[삼각함수] 일반각과 호도법

 

결국 삼각함수 전체의 내용의 흐름은 집합과 같습니다.

고1 집합 단원에서 여집합 차집합 드모르간의 법칙을 외워서 식을 정리했던

그것과 정말 정확히 똑같은 단원입니다.

 

그래서.. 이런 말 하면 안돼는거 압니다만, 삼각함수는 완벽한 암기과목입니다.

이해해도 못 외우면 아무것도 못하지만, 이해 못해도 외워두면 사용할 수 있습니다.

 

---

[일반각]

 

1)정의

 

 

·시초선 : 움직이지않는 각의 기준선

·동경 : 시초선에서 시작하여 일정거리만큼 회전한 사선

·일반각 : 각도 + 방향 + 회전수로 표시한 각도의 일반적인 총 정보

·양의 방향 : 시계 반대방향 (그림의 방향입니다.)

·음의 방향 : 시계 방향

 

※추가설명

회전수 360°x n 에서 n은 정수만 취급합니다.

---

2)일반각의 사분면 범위

 

 

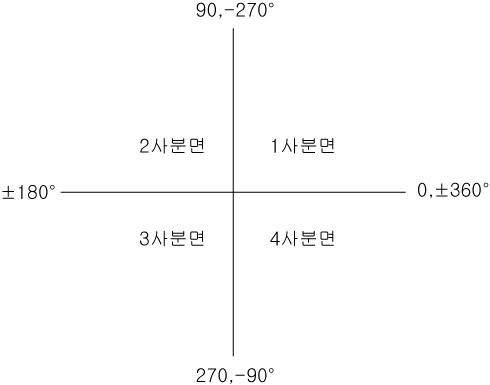
동경이 1사분면에 있기 위해선 음과 양의 방향에 따라

① 360°x n + 0° < x < 360°x n + 90°

② -360°x n + 0°  < x < -360°x + 90°

※n은 임의의 회전수 (정수) 입니다.

 

즉 , 몇바퀴를 돌았는가에 대해서 바퀴수만 같다면 , 0° < x < 90° 일때에 성립합니다.

 

※추가설명

-360°x n - 270°  > x > -360°x (n+1) 로도 표현은 가능하지만

일반각에 쓰이는 360n+θ° 에서 θ° 는 계산상 편의를 위해서 주로 양수를 사용합니다.

 

---

3)두 동경의 관계 {암기}

 

①핵심 요약 (α , β는 일반각의 크기)

 

두 동경이 

→

일치 : α - β = 360° x n
일직선 : α - β = 360° x n + 180°
x축 대칭 : α + β = 360° x n
y축 대칭 : α + β = 360° x n + 180°
y=x축 대칭 : α + β = 360° x n + 90°
y=-x축 대칭 : α + β = 360° x n + 270°

 

②그림 설명

 

⑴두 동경이 일치

 

⑵두 동경이 일직선

 

⑶두 동경이 x축 대칭

 

⑷두 동경이 y축 대칭

 

⑸두 동경이 y=x축 대칭

 

⑹두 동경이 y=-x축 대칭

 

---

[호도법]

 

1)정의

 

 

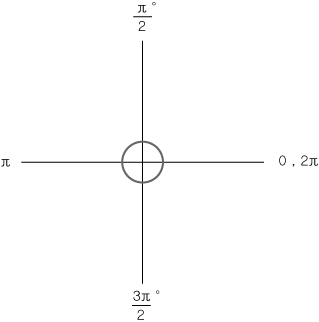
육십분법은 60진수를 사용하기 때문에 1'(초) 미만의 각도를 다루는데에 불편함이 따릅니다.

그래서 원의 반원의 반둘레 ÷ 반지름 인 π를 중심으로 각도를 표현하는 방법이 호도법입니다.

 

---

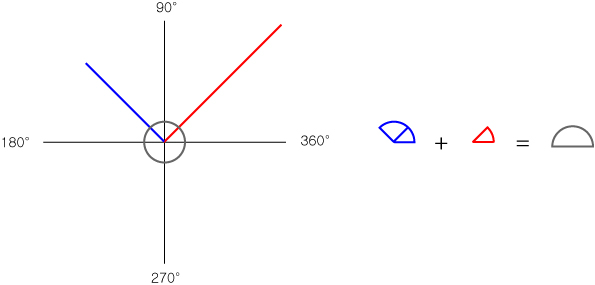
2)일반각⇔호도법

※설명을 위하여 호도법의 임의의 각도를 이번만 θ' 라고 적습니다.

 

① 360°x n + θ° = 2nπ + θ'

② θ°→θ' = x° * π/180°

 

---

3)호도법과 삼각비

 

① 30°

 

② 60°

 

③ 90°

 

④ 180°

 

---

4)호도법의 부채꼴 넓이

 

호도법을 사용할 경우 추가적인 식정리로 부채꼴 넓이 공식 다르게 정리됩니다.

 

기존공식 S=½rl (l=호의길이)

r²π x 1을 2 x ½ 로 두고 ½r·2rπ 로 둡니다.

그런데 2rπ는 원의 둘레 공식이고 원의 둘레에 θ°/360° 를 하면 부채꼴 호의 길이가 될 것입니다.

 

다만 이 공식을 사용하기엔 호의 길이를 따로 계산해야 하기 때문에 불편함이 있지만..

 

변형공식 S=½r²θ

l=rθ 가 적용된 공식입니다.

생각해봅시다.

π는 반원의 호의길이 / 반지름 이였죠? 그래서 반지름만 다시 곱하면 호의 길이가 나옵니다.

호도법은 π를 기준으로 하기 때문에 이런 정리가 가능해집니다.

 

---

2.응용

 

[기본]

 

① -120° = 360°x n +240°

② 5/4<n<5/2 일때 회전수 n은 정수이므로 2

 

---

[확장 지식]

 

일반각의 사분면 범위를 약분한다면

360°n+180°<a<360°n+270° 이를 ⅓배 한다면

120°n+60< a/3 <120°n+90°

 

1n당 120° 이므로 3n+1n,2n,3n(=0n) 단위에 따라 동경이 다른 사분면에 위치합니다.