-
[지수와 로그] 로그 함수수학/고2 2022. 10. 30. 13:50
지수함수와 굉장히 유사한 개념을 지니고 있기 때문에
지수함수에 대해서 알고 있다면 가볍게 넘어갈 수 있습니다.
그래프 이미지에서 환 공포증이 발생할 수 있으므로 주의해 주시길 바랍니다
1.개념

x-m은 로그의 진수로 사용된 숫자, n은 상수항입니다.
m은 x축 평행이동 , n은 y축 평행이동을 의미합니다.
1)제약조건
①a(밑)>0 , a≠1 → 로그의 제약 조건과 같습니다. (X>0은 아래 추가설명을 확인해주세요.)
②log₂X² ≠ 2log₂X → x²의 근과 ±x가 되므로 제약이 있습니다.
③log₂X³ = 3log₂X → 진수의 지수가 홀수일때 근은 음근으로 변화하지 않으므로 제약이 없습니다.
※추가설명
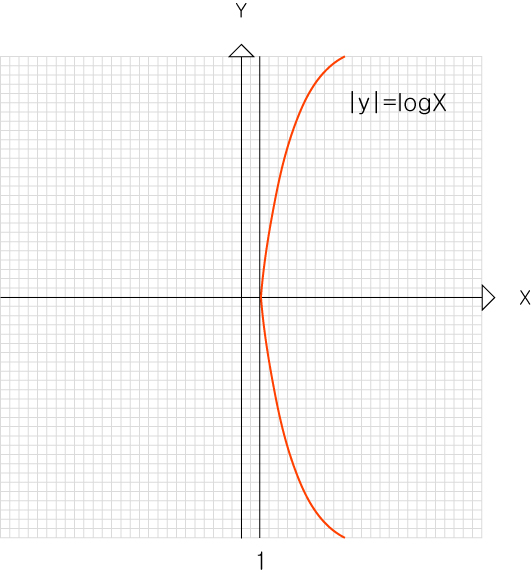
만약에 log₂X²를 그래프로 그린다면 일반적인 로그 그래프를 y축에 대칭한 우함수 모습이 됩니다.
로그 제약에 의하면 X는 음수가 될수 없으나,
X²에 대해서는 X가 음수일때로 양수로 변환되므로 그래프 표현이 가능해집니다.
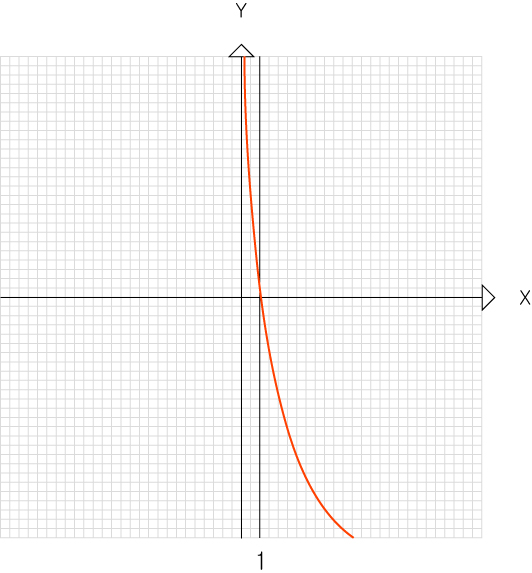
2)로그 그래프
① a>0

② 1>a>0
3)로그 그래프 특성
①진수 x=1 로 만드는 지수y의 값은 언제나 0이므로 언제나 (1,0)을 지나갑니다.
②(1,0)이 점을 그래프의 대표점 이라고 합니다.
③평행이동에 의해 대표점은 (1+x,y)가 될수 있습니다.
④특정범위의 최대 최소는 양끝 혹은 진수식 logƒ(x) 의 최대 최소값이 됩니다.
⑤그래프의 밑a 가 작을 수록 그래프가 가파르게 변화합니다.
※logƒ(x)에 대해선 지수 함수의 [확장지식]을 참고해주세요
4)로그함수의 성질
①y = log½X → -y = log₂X
②f(xy)=f(x)+f(y)
③f(x+y)≠f(x)f(y)
④logX² = 2log|X|
※추가설명
②:logCX는 logX+logC 이므로 logX를 logC만큼 y축 평행이동한 그래프입니다.
진수 조건에 의해서 밑 a는 0,1 이 될수 없으므로 +logC 반드시 평행이동을 한 상태가 됩니다.
[확장 지식]
1.지수함수의 계수는 평행이동을 의미한다.

2.로그(이차식)의 최대/최소값
Log(이차식) 일때 이차식에 대한 완전제곱식으로 최대나 최소수치를 구할 수 있다.
다만 (Log)²일때도 최대 최소값을 지니고 있다.
[변형 그래프]
①
②

'수학 > 고2' 카테고리의 다른 글
[삼각함수] 일반각과 호도법 (0) 2022.10.31 [지수와 로그 完] 로그 방정식과 로그 부등식 (0) 2022.10.30 [지수와 로그] 지수 방정식과 지수 부등식 (0) 2022.10.29 [지수와 로그] 지수 함수 (증가함수 , 감소함수) (1) 2022.10.29 [지수와 로그] 로그와 상용로그 (0) 2022.10.28