-
[삼각함수] 삼각함수 그래프수학/고2 2022. 11. 1. 17:19
1.개념
[주기함수]

1.정의
반복운동하는 그래프함수를 주기함수라고 합니다.
그중에서도 상하 운동을 하는 주기함수를 진동함수라고 합니다.
여기에서 주기란 , 반복운동의 최저점 사이의 거리를 의미합니다.
p는 주기의 정수배 라고 합니다.
2.주의사항
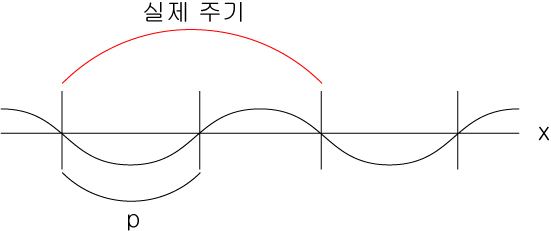
함수표기로 f(x) = f(x+p) 일때 주기함수를 만족합니다.
그러나 p의 크기에 따라서 주기가 아니임에도 일부 만족할수 있기 때문에
임의로 구한 주기p가 주기가 맞는지 f(x+1)에서도 확인해야 할 수 있습니다.
그림에서 p는 주기의 사이값 이라고 합니다.
[삼각함수 그래프]
1.그래프 모양
핵심만 설명하자면
삼각함수의 값은 -1과 1을 향해서 왓다갔다 반복운동을 합니다.
갑자기 값이 급변하는 구간은 없고,
일차함수처럼 값이 오르고 내리는 속도가 동일하지도 않습니다.
sin의 시초선에서의 값은 0, (y의 높이는 0)
cos의 시초선에서의 값은 1, (x의 너비는 1)
tan의 시초선에서의 값은 0 (기울기는 0도)
그러므로
① y=sinX (시초선의 값은 0)
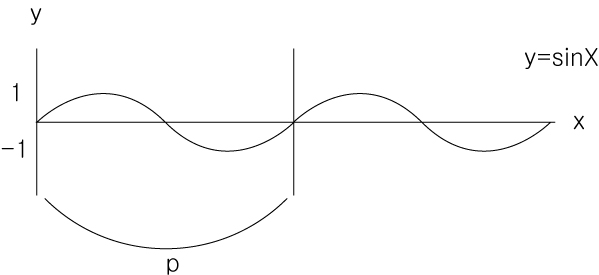
② y=cosX (시초선의 값은 1)
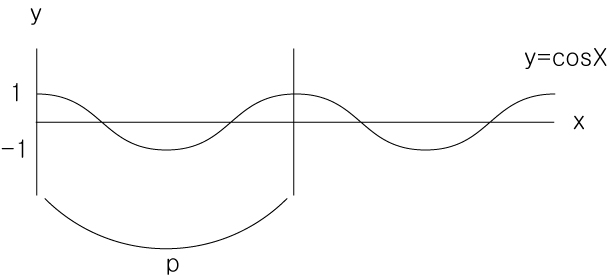
※cosX의 모양은 sinX를 평행이동한 그래프입니다.
③ y=tanX (시초선의 기울기는 0)

tan의 주기가 sin과 cos 보다 반으로 짧은 이유는
3사분면으로 이동하면서 기울기가 다시 1사분면과 같아지기 때문입니다.
y=(-삼각함수X) 에서 위의 그래프들은 상하 반전이 됩니다.
2.함수식의 구성 {암기}
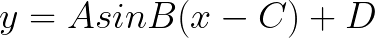
sin,cos,tan 모두 같은 식을 공유합니다. ①각 요소들의 의미
A:진폭(기울기)
B:주기속도
C:좌우이동
D:상하이동
②주기와 진폭
⑴sin , cos
주기 : 2π/|B|
진폭 : D±A
⑵tan
주기 : π/|B|
중심높이 : D
3.그래프의 대칭지점 {암기}
π(180°)에 n이 곱해지는 이유는 각 주기마다 값이 같기 때문입니다.
①sinX
대칭점 : nπ (중심선의 위치)
대칭축 : nπ+π/2 (주기의 최고점, 최소점 위치)
②cosX
대칭점 : nπ+π/2
대칭축 : nπ
③tanX
대칭점 : nπ
점근선 : nπ+π/2 (p=π에서 π/2 즉 각 주기의 절반지점)
2.응용
[확장 지식]
1.삼각함수는 우함수 , 기함수 이므로 함수식이 적용 가능하다.
기함수 : ƒ(x) = -ƒ(-x) → tan(-π) = -tan(π)
우함수 : ƒ(x) = ƒ(-x) → cos(-9π) = cos(9π)
※sin : sin(-2x)=-sin2x
※기함수와 우함수는 x=0을 기준으로 하고 있습니다.
2.주기의 정수배를 구하는 방법 {다소 이해력 필요}
y=sin(5/2x) 일때 y=sin5/2(x)로 정리됩니다.
이때 5/2를 B로 주기를 구하면 '4/5π' 이며
(4/5π)n 주기가 정수가 되는 부분까지 필요한 n=5 입니다.
즉 , y=sin(5/2x)는 ƒ(x+5)=ƒ(x)를 만족합니다.계산과정의 특징상 약분이 안됀다면 정수배는 주로 분자가 됩니다.
[기본]
①함수의 주기가 4
f(x) = f(x+4)
②삼각함수 식 구분하기
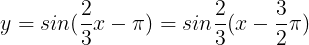
주기는 2π/|2/3| 이므로 3π가 됩니다.
③첫번째 주기는 두번째 주기 - 주기
첫번째 중심값은 x의 평행 이동량 알수 있기 때문에
그래프로 식을 추정할때 첫번째 주기를 알아내야 하는 경우가 있습니다.
[테크닉]
주기 π , 2π에 의한 정리

[변형 그래프]
※cos 은 sin을 평행이동한 그래프이므로 제외했습니다.
①
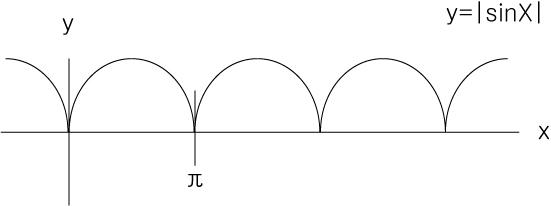
주기가 π가 되며 기함수없이 우함수만 만족하게 됩니다.
②
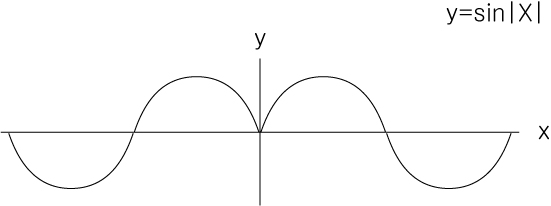
0의 지점에서 주기가 성립하지 않는 우함수가 됩니다.
③

④
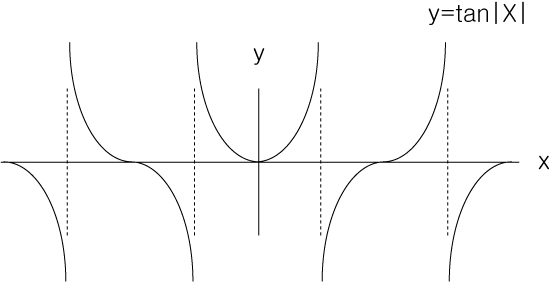
'수학 > 고2' 카테고리의 다른 글
[삼각함수] 삼각방정식과 삼각부등식 (0) 2022.11.02 [삼각함수] 삼각비간의 교환과 대칭 (0) 2022.11.01 [삼각함수] 삼각비와 삼각함수의 관계 (0) 2022.10.31 [삼각함수] 일반각과 호도법 (0) 2022.10.31 [지수와 로그 完] 로그 방정식과 로그 부등식 (0) 2022.10.30