-
[삼각함수] 삼각방정식과 삼각부등식수학/고2 2022. 11. 2. 19:01
삼각비를 못 외웠다면 진행이 안됩니다.
이게 어떻게보면 다행일지도 모릅니다.
그 삼각비 에서 정해준 숫자들 외에는 등장하지 않는다는 뜻이니까요.
1.개념
[삼각 방정식]
1.정의

생각해보면 sin 함수는 반복되는 주기함수입니다.
1/2을 만족하는 지점이 +2π 마다 반복됩니다.
그래서 삼각 방정식은 기본적으로 x의 크기에 대한 범위가 존재해야 합니다.
2.풀이
이하의 과정들은 sinX가 양수라는 것을 기준으로 삼고있습니다.
작성되어있는 값들이 -sinX에서 반전되어 위치가 다를 수 있음을 기억합시다.
①양수에 대한 방정식의 해

해를 구할때, 그래프 이미지를 중심으로 생각해서 구할 필요가 있습니다.
y=½ 과 y=sinX의 첫 교점은 (0~2π) 내에 sinθ = 1/2 을 만족하는 ∴ π/6 (30°)
0~π/6 와 사잇값~(π-π/6) 간의 x축 거리가 같으므로
또 다른 교점은 π-π/6 = (5/6)π로써 범위내의 해는 총 2개가 됩니다.
x의 범위가 더 넓다면 주기 간격으로
[첫번째교점 + n2π] 와 [두번째 교점 + n2π] 단위로 해의 갯수가 증가합니다.
②음수에 대한 방정식의 해

구하고자하는 y축 교점이 음수라면 양수에서 구한 두 근에 + 사잇값(π)을 하면 됩니다.
이런 이유로 sinX=K 같이 음양을 알수없는 미지수는
해가 존재하는 범위가 x의 부등호범위인 0~2π로 넓어집니다.
역으로, 범위가 π+α , 2π-α 라고 한다면 k는 음수가 된다고 할 수도 있습니다.
③삼각함수의 연립방정식

삼각함수=ax+b 일땐 직선이 기울기를 지니므로 범위의 지정이 필요하지 않습니다.
그래서 그래프의 모양을 추정하여 해의 갯수가 몇개인가를 추청할 수는 있습니다.
다만, 계산하여 해를 구하는 과정은 어디에도 없습니다.
이유는 sinX 에서 sin을 제거하고 X만 남길 방법이 없기 때문에 해를 구할 수 없기 때문입니다.
(혹은 작자가 모르는 수학의 영역일지도 모르겠습니다.)
[삼각 부등식]
1.정의

2.풀이
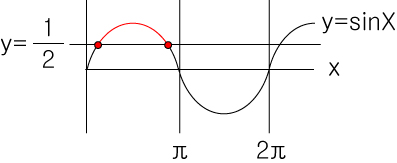
∴ π/6 < x < (5/6)π
삼각 부등식은 주로 두 해와 값½ 의 부등호 관계를 의미합니다.
2.응용
[확장지식]
1)tan X (x≤π)
tan 는 π 마다 값을 지니지 않는 점근선이 존재합니다.
그러므로 ≤의 등호가 성립하지 않아서 x<π로 다시 판단합니다.
2)x의 범위와 삼각함수의 최대최소값
sinX(0<x<π) 일때 그래프는 양수만 존재합니다.
그러면 이때 y값인 sinx 의 최대 최소값은 0<sinx<1가 됩니다.
3)삼각함수의 이차식 근
삼각 함수가 들어간 이차식은 삼각함수의 최대최소범위에 의해서 값이 제한됩니다.
2(cos-½)(cosx+3)=0 → ∴cosx = 1/2 , -3.
그런데 -1≤cos≤1 이므로 -3이 제외되어 해는 cos=1/2 하나가 됩니다.
4)삼각함수의 완전제곱식
완전제곱식 (t-1)²-2=k 에서 -1≤t≤1 일때 최소값 k의 범위는 -1,1을 대입한 -2≤k≤2 가 됩니다.
[심화]
※심화는 어렵지만 알아두면 좋은 확장 개념을 담고 있습니다.
x를 품은 t의 그래프
①t의 범위의 변동
t=3x+π , 0<x<π 일때
0<3x<3π → π<t<3π+π 로 정리됩니다.
②y=sin t 의 그래프

만약 x의 범위가 무한대라면 t 도 무한대 까지의 최대 최소범위를 지니고 있겠죠?
그렇다면 t의 값에 따라서 sin t 로 그래프를 그린다면,
t=0 일때 sin 0 = 0 , t=π/6(30°와 같은 값) 일때 sin30°=1/2
으로 sin x 와 모든 동일한 값들을 지니고 있다는 뜻입니다.
즉 , y=sin t 가 y=sin x와 다를게 없습니다.
③y=sin t 의 그래프 범위
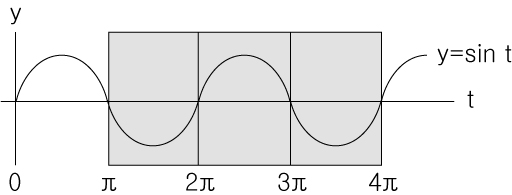
이 그래프에서 t내부의 x값이 0<x<π 의 제한이 있다고 해봅시다.
아까전에 변형에 의해서 t의 범위는 π<t<4π 를 지닌다고 했으니.
그래프에서 해당하는 범위는 칠한 범위에 속하게 됩니다.
③y=sin t 에서 x의 값 추정하기
위의 그래프에 따르면 y=1일때의 t의 값은 (5/2)π 입니다.
그렇다면 t=(5/2)π 즉, 3x+π = (5/2)π니까 정리하면 x의 값이 나올 것입니다.
[기본]
①
y=3sinX+1 일때 -3≤y≤3 이므로 최대최소값은 3+1,-3+1
②
y=|2sinX| 일때 -1≤sin≤1 에서 최대값은 |2*1| 혹은 |2*-1|
③
5/(t+3)-1 , t=sinx 일때 (-1≤t≤1) 에서 최대 값은 5/(-1+3-1) = 5
[테크닉]
①
tan+√3cot=1+√3
→ tan를 양변에 곱하면 tan²-(1+√3)tan+√3=0
※추가설명
이 부분은 워낙에 변형이 많아서 하나만 추려봤습니다.
말하고자 하는 핵심은 삼각비간의 변환 공식으로
tan↔cos↔sin 으로 변형하여 한가지로 통일할 수 있지 않은가를 확인하라는 뜻입니다.
또한 분모로 간 삼각비 역수도 이 변형의 범위에 포함 되므로 더 주의하라는 뜻입니다.
'수학 > 고2' 카테고리의 다른 글
[수열] 수열의 정의 (short) (0) 2022.11.03 [삼각함수 完] 삼각함수의 공식 (증명 無) (0) 2022.11.02 [삼각함수] 삼각비간의 교환과 대칭 (0) 2022.11.01 [삼각함수] 삼각함수 그래프 (0) 2022.11.01 [삼각함수] 삼각비와 삼각함수의 관계 (0) 2022.10.31