[지수와 로그] 선행 - 거듭제곱근

 

먼저 배워놔야만 지수를 들어갈수 있기 때문에 정규과목에서 첫번째로 배우는 과정입니다.

주제와 조금 떨어진 내용이지만 기타 과목에서 같이 다루지않은 이유는

앞선 내용들과 달리 개념 설명이 다소 필요하기 때문입니다.

---

1.개념

 

[거듭 제곱근]

 

0)핵심 요약

ⓐ²√2²=2

ⓑ³√(-3)³ =-3

ⓒ⁴√(-2)⁴=2

---

1)정의

ⓑ에서 ³√ 에 해당하는 부분이 거듭제곱근 입니다.

³√27 는 세번곱해서 27를 만들수있는 숫자 3 (3 x 3 x 3 = 27)을 의미합니다.

---

2)읽는법

⁴√4⁴

네 제곱근 4의 네 제곱

 

※부가설명

4의 네 제곱근 네 제곱 =(±⁴√4)⁴  

---

3)음양의 우선순위

지수가 홀수일때 음수 , 짝수일때 ±√a 가 됩니다.그 중에서 허수는 정의에서 제외됩니다.

 

※부가설명

1)4의 네제곱근에서 -2 +2를 쪼개면 (-√2 , √2) , (-√2i , √2i) 이때 ±√2 만 사용한다는 의미입니다.

2)a의 네제곱근은 ± ⁴√a 세제곱은 ± ⁴√b³즉, 4제곱근 4제곱은 ±수치가 제곱시에 양수만 남기 때문에 양수입니다.

---

4)거듭제곱근의 실근의 갯수

 

ⁿ√a	a<0	a=0	a>0
n=홀수	1개	1개	1개
n=짝수	0개	1개	2개

 

ⓐ짝수 함수 그래프

 

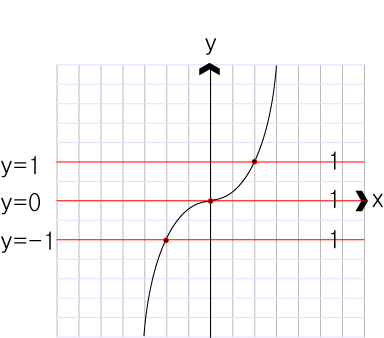
ⓑ홀수 함수 그래프

 

※부가설명

1)y=xⁿ (n은 상수)는 가속증가, y=ⁿ√x도 x값이 높을 수록 가속증가입니다. 즉, 모양이 같습니다.

2)단일항 그래프이기 때문에 그 모양은 우함수(짝) 기함수(홀)를 반복합니다.

 

---

5)거듭제곱근 계산방법

 

x²+x+1 은 허근이므로 제외됩니다.

---

6)거듭제곱근의 성질 {암기 단원}

 

①

ⁿ√3 > ⁿ√2 (대소관계)

 

②

√2 = ⁴√2²

 

③

√2 = ²√2

 

④

²√2 * ²√2 = ²√2²

 

⑤

⑥

²√(2²) = (²√2)²

 

⑦

 

⑧

 

---

2.응용

 

[테크닉]

 

①2 * ³√2= ³√2³ * ³√2 = ³√2⁴

 

②2 ? ²√3 → ²√2² > ²√3 (대소관계 파악)