[~고1] 잊기 쉬운 기초 정리

 

고1까지의 지나온 과정들을 다시 살펴보는 이유는 고2 이상의 과정이 지니는 특수성 때문입니다.

 

고2에 접어들면서 마주하게될 문제들의 의도는 수능을 기준으로 하기 때문에

'당신이 이걸 풀수 있는가'를 목적으로 하는 문제의 비중이 상당히 높습니다.

 

'적분은 이렇게도 사용할수 있다' 를 알려주는 문제가 줄어들고

'적분을 하고 싶다면 알고있는 방법으로 식을 먼저 구하고 변형하세요' 같은 문제가 늘어납니다.

그래서 배우는 과목과는 무관하게 이전에 배운 다른 개념들을 집고 넘어갈 필요가 있습니다.

 

아래에 나열할 개념들은 앞서 고1까지 간단하게 언급하고 넘어가기에 잊어버리고 넘어가기 쉬우나

문제를 해결하기 위해선 필요한 지식들만 모았습니다.

 

판별식 D , 완전제곱식 , 함수대칭 , 그래프이동 , 항등식 등의 메이저한 수학 지식들은

다시 다루기엔 양이 많기 때문에 만약 모른다면 다시 공부 하셔야 진행할 수 있습니다.

 

 

"수능의 변별력 문제가 한국의 수학수준을 망친다."

---

[복습]

 

1.부분분수

 

 

1-2 삼중 부분분수

 

 

2.역함수의 성질

 

▷f(a)⁻¹ = a

▷(f(a)⁻¹)⁻¹ = f(a)

▷y=x에 대한 대칭

 

3.각종 평균

 

 

3-2. 산술평균>기하평균 (절대부등식)

 

▷{x+y}/2 ≥ √xy
= x+y ≥ 2√xy
= x²+y² ≥ 2xy

 

→x≥0 , y≥0 일때 x+y의 최소값은 2√xy

 

4.가우스 그래프

 

→가우스 그래프는 반드시 정수 부분마다 끊긴 모양을 하고 있다

 

5.절대값 식 정리

 

①|-2x²-x| = x|-2x-1|

②m|x|+1=5 → |x|=4/m → x=±4/m

 

6.모든항이 미지수인 함수표현

 

▷2차방정식 

①ax²+bx+c

②a(x-m)(x-n) : 두 근이 m,n인 2차방정식

→교재에선 두 근을 α,β로 쓰므로 a,α의 혼동에 주의

 

▷3차방정식

①ax³+bx²+cx+d

②a(x-m)(x-n)(x-l)

③a(x-m)²(x-n) : 두 근이 m,n인 3차방정식

 

7.축의 방정식

▷2차방정식의 두 근이 0 , 2 일때 축의 방정식은 x=1

 

8.허수법칙

 

 

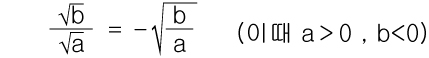
9.원에 내접하는 사각형

 

 

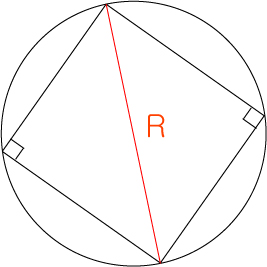
▷대각의 합이 180° 일때 사각형은 원에 내접하다.

▷대각의 합이 180°인 두각 사이의 대각선은 원의 지름이 된다.

 

10.역함수의 곱

▷(f(x)*g(x))⁻¹ = f(x)⁻¹*g(x)⁻¹

 

---

[독해]

1.f(x)≤0

> f(x)의 최소값은 0보다 작을것이다.

 

2.두 그래프가 한점에서 만난다

>f(x)=g(x)로 표현할 수 있다.

3.y=f(x),y=g(x) 가 x=2 에 대하여 대칭한다.

>f(2)=g(2)

4.f(x)=kf(y)를 만족 or x,y가 모든실수에서 만족하는식

>x=y=0을 대입