[기타]고2 과정에서 배우는 작은 개념들

 

진도와는 상관없이 수학을 하면서 부가적으로 알려주는 여러 작은 지식들이 있습니다.

혹은 진도와는 약간 떨어지지만 알고 넘어가야만 하기에 집고 가는 지식들도 있습니다.

혹은 알고 지나가야 하지만 알려주지않고 눈치껏 배워야하는 지식들도 있습니다.

이번에 다루는 글은 그런 기타 개념들을 한곳에 모았습니다.

 

1장 [지수와로그] 는 다룰 부분이 없어서 제외했습니다.

 

당장에는 완벽하게 이해할수 없는 설명은 주황색 표시를 해놓습니다.

주황색은 이게 어떤것을 말하려는 느낌인지 감만 잡아둬도 쓸수 있는 지식들입니다.

빨간색은 매우 중요하기 때문에 반드시 숙지하지 않으면 힘들어 지는 지식입니다.

---

1.[지수와로그]

 

2.[삼각함수]

 

1)육십분법

→정삼각형의 각도를 60도라고 기준을 잡고 각도를 표현하는 방법입니다.

→시계가 60분에 1시간인 듯이 정삼각형의 각 하나당 60°로 표현한 것입니다.

→피라미드의 건축에서 유래 되었다고 전해집니다.

 

2)1도 1분 1초

→1° = 60'(분) = 360"(초)

→시간을 의미하는 것이 아닌 각도를 의미합니다.

→훗날 시계의 기준이 되었습니다.

 

3)보각

 

 

→180도를 기준으로 부족한 각의 크기를 의미합니다.

→π-θ

 

4)여각

 

 

→90도를 기준으로 부족한 각의 크기를 의미합니다.

→π/2-θ

 

5)대변 (그 대변아님)

 

 

→붉은 표시를한 각에대한 대변은 빨간 변입니다.

→반대로 선에대한 각은 대각 이라고 합니다.

→변과변 , 각과 각 사이에서도 사용되는 단어입니다.

 

6)둔각의 삼각비

 

 

→이경우 180-120=60°로 취급됩니다.

→둔각이 180°를 넘어가면 각도는 -각도 (아래쪽의 각도)를 지닙니다.

→음의각도에서 둔각을 이루면 (-180°)-(180-둔각)으로 취급됩니다.

 

---

3.[수열]

 

1)아래첨자 해석

 

①

⇒A={4,5,6} 에서 a₁=4 , a₂=5 , a₃=6

▷함수가 지니는 원소의 순서를 의미합니다.

 

②

▷아래첨자가 쓰인 식은 언제나 최소단위를 기준으로 합니다.

▷즉, 곱하는 미지수가 둘다 첨자를 쓴다면 k₁a₁로 씁니다.

 

③

⇒a₁은 언제나 첫번째 항의 기준을 의미하기 때문에 아래첨자는 음수가 될 수 없습니다.

▷다만, 개념적으로 0번째 항을 가정하여 쓰이는 경우가 존재합니다.

▷아래 첨자는 언제나 정수이므로 미지수로 표현할때 n을 사용합니다.

 

④

 

▷등식으로 묶인 두 첨자 n은 항상 같은 숫자를 유지합니다.

 

⑤

 

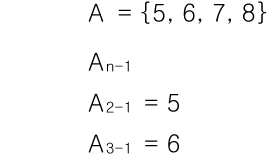
▷첨자는 식을 구성할 수 있습니다.

▷단, 음수가 될수 없기 때문에 정의역의 제한이 존재합니다.

 

2)자연수 합의 공식

 

① 1+2+3+…+n = n(n+1)/2 

 

② 1²+2²+3²+…+n² = n(n+1)(2n+1)/6

 

③ 1³+2²+3²+…+n³= (n(n+1)/2)²

 

3)피보나치 수열 (코딩테스트에 밥먹듯이 마주하는 수열)

⇒F = {1,1,2,3,5,8,13,…}

→첫째항과 그 다음항의 합으로 구성되는 수열입니다.

 

4)축차대입법

미지수 첨자 혹은 미지수에 1~n까지 숫자를 대입해서 등식이 맞는지 확인하는 방법입니다.

 

---

3.[극한]

 

1)부등호 범위의 함수

 

→부등호에 따라서 기울기와 위치가 달라지는 지점이 존재하는 함수입니다.

→식은 3개 이상이 될수도 있으며 이에 따라서 급변하는 지점이 다수 존재할 수 있습니다.

→식이 정해져있지않은 ƒ(x)가 특정 조건에서 연속하는 가에 대한 반례로 사용됩니다.

＊tmi 1. 앞으로 숨쉬듯이 계속 만나게될 함수이지만 이름이 존재하지 않습니다.

＊tmi 2. 그래서 작자는 이 함수를 조건함수라고 부르고 있습니다.

 

---

4.[미적분ⅰ]

 

1)기함수와 우함수

 

①기함수의 식 : ƒ(x) = -ƒ(-x)

→ƒ(-x) = -ƒ(x) , 즉 원점 대칭에 의해  x와 y의 부호가 반전된 값과 원래값이 같습니다.

→홀수 함수라고도 합니다.

 

②우함수의 식 : ƒ(x) = ƒ(-x)

→즉, y축에 대해서 좌우의 식에 대한 값이 같습니다.

→짝수 함수라고도 합니다.

 

③기함수 x 우함수 = 기함수

 

④삼차함수가 기함수일때 ax³+bx

 

⑤ƒ(x)가 기함수일때 ƒ'(x) ↔ ƒ(x) ↔ F(x) 에서 ƒ'(x)는 우함수 F(x)는 우함수

 

---

5.[기타]

 

1)음의 약수

→ 3= 1x3 혹은 -1x-3

 

2)모든 양의 약수의 합공식

→ (1+a+aⁿ)*(1+b+bⁿ) (a,b는 소인수 , n은 해당 소인수의 갯수)