[~고1]기초 변형 및 계산 테크닉

 

이하의 내용은 고1까지의 과목들을 응용하여 다음과 같이 구성되어 있습니다.

 

기초는 반드시 알고 있어야 되는 내용 [6문]

응용은 특정 지식을 중심으로 진행되는 흐름 [2문]

활용은 지식을 보조하는 부가정보 [2문]

해석은 문장이나 식의 진의 [6문]

테크닉 은 식 정리 [7문]

변형은 개념에 의해 변형된 식과 그래프 (가장 어렵습니다.) [10문]

 

선정은 단순히 어려움이 아니라 계산법을 모르면 손을 댈 수 없는 지식과

반드시 알아야 되는 계산법을 기준으로 합니다.

이를 무시하고 진도를 뺄지 아니면 한번 둘러보고 고민할 시간을 아낄지는 스스로의 판단에 맡깁니다.

 

---

※ ▷문제의 식 , ▶풀이

 

1.[기초]

 

1)차수 낮추기 , 차수 올리기

▷a²=a-⅓ → a³=a²-⅓a (차수 올리기)

▷t⁴-6t³+12t²=mt → t³-6t²+12t=m (차수 내리기)

 

2)F(0)=C (ax²+bx+c)

▷F(0)-G(0)=-3

∴ G(x)=F(x)+3

 

3)근은 대입시 0으로 만드는 수를 의미한다.

▷x³-2x+k = (x-α)(x-β)(x-γ)

∴ a³-2a+k=0 → k=a³-2a

 

4)여러개의 x에 대한 부등식은 하나로 합쳐진다.

▷t<-1 , t>A

∴ (t+1)(t-A)>0

 

5)분수함수의 정리

 

 

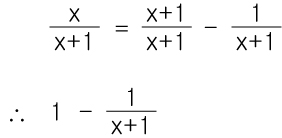
6)x≠α의 근

▷(a-b)(k+2(a+b))=0 (a≠b)

∴ k+2(a+b)=0   ∵ (a≠b)

 

---

2.[응용]

 

1)함수식을 사용한 근과 계수의 관계

▷f(0)*f(0)=-1 , f(0)=a , a²+a+k=0

▶a=f(0)이므로 두근의 곱은 K=-1    

▷ƒ(x)+g(x)=x²+4x+C , ƒ(x)g(x)=x(x+2)(2x-1)

▶두 근의 합에서 4x가 되기 위한 ƒ(x),g(x)의 쌍은 (x(x+2) , 2x-1)

 

2)함수에 대한 대한 기함수 , 우함수 판단 {함수의 대칭}

▷ƒ(x+y)=ƒ(x)+ƒ(y)

▶y에 -x를 대입하면 ƒ(0)=ƒ(x)+ƒ(-x)

▶y=x=0을 대입하면 ƒ(0)=ƒ(0)+ƒ(0)   ∴ƒ(0)=0 (아래 후술)

▶ƒ(x)+ƒ(-x)=0 → ƒ(-x)=-ƒ(x) (기함수)

 

---

3.[활용]

 

1)반원의 이차함수

 

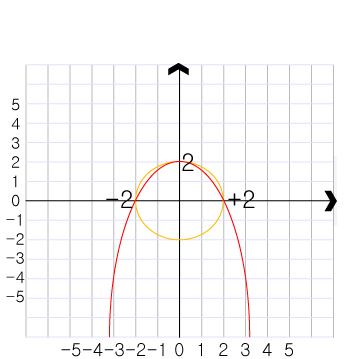
이차함수는 기울기가 수직이 될수 없으므로 곂치지 않습니다.

 

※설명하는 내용은 사물과 도형들을 좌표평면에 두는 방법입니다.

▷원의 반지름이 2일때 원을 원점에 두면 반원에 대한 이차함수를 구할 수 있습니다

▶a2²+b2+2=a(-2)²-b2+2=0

∴y=½x²+2

 

2)일차함수와 이차함수의 교점의 비

 

 

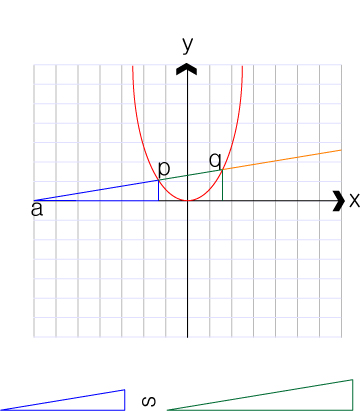
▷ƒ(x)=이차함수

▷직선 apq 에서 ap:aq=1:4 라면 높이인 ƒ(p):ƒ(q)=1:4 가 됩니다.

---

4.[해석]

 

1)함수조건에의한 중심축

▷ƒ(1-x)=ƒ(1+x)

∴ 방정식은 중심은 x=1    ※1에 대칭하는 함수, 2차함수일때 축의 방정식

 

3)항상 위에있는 함수

▷f(x)가 g(x)보다 항상 위에있다면 f(x)>g(x) 라고 표현할 수 있습니다.

▷f(x)-g(x)>0

 

4)ƒ(0)가 들어간 식의 정리 (ax²+bx+c)

▷ƒ(0)=3ƒ(0)ƒ(0)

▶3ƒ(0)를 1 로 만들기 위해서 곱해야돼는 수는 1/3 이므로 ƒ(0)=1/3

▷ƒ(0)=ƒ(0)+ƒ(0) → ƒ(0)=0

▷ƒ(0)=ƒ(0)+ƒ(0)-1 → f(0)=1

 

5)두함수의 정비례

▷f(x)의 기울기가 x²와 정비례 하기 위해선 f(x)=ax²

 

6)ƒ(x) 가 g(x)로 나누어 떨어진다면 

▷ƒ(x)=x³+ax²+bx+c, h(x)=(x+1)(x-2) , f(x)÷g(x)=k ...0

▶ƒ(-1)=0 , ƒ(2)=0        ※ƒ(x) = (x+1)(x-2)(x-α)

 

---

5.[테크닉]

 

1)

 

 

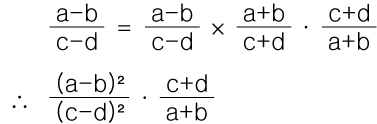
2)

 

 

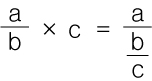
3)

 

 

4)

 

 

5)

▷x²-3x=3ax

▶x²-(3+a)x=0

▶x(x-(3+a))

∴ x=3+a , x=0

 

6)

 

 

7)

▷-2t-at-3=1, -t²+2=at²+3t

▶-2t-at-3=1 →  at=-t-2

▶ -t²+2=(at)t+3t → -t²+2=(-t-2)t+3t

∴  t=2

 

---

6.[변형]

 

 

1)합과 곱의 변형 {산술평균>기하평균}

▷ƒ(x,y)=x²+y²-2xy
▶x²+y²-2xy≥2xy-2xy

※(x+y)²≥4xy → x²+y≥4xy-2xy

 

2)가우스의 정의와 식{가우스 , 이해력 다소 필요 , HARD} ▶이해필요 ▶어려움

▷[x]는 x보다 크지않은 최대정수

▶x=[x]+a    ※a는 양수 혹은 음수

▶[x]=x+a    ※a는 양수 또는 음수이므로 +로 표현해도 같다.

▶[x/3] = n  →  x=3n+a    ※위의 주황식이 적용됩니다.

▷[-x] = -n-a → -n(-1+1)-a     ※-n-1은 정수부 1-a는 소수부가 됩니다.

▶[-x] = -n-1     ※가우스는 소수부인 1-a가 없는 숫자를 의미합니다.

 

 

3)무리수의 가우스 그래프 {허수 , 가우스}

 

 

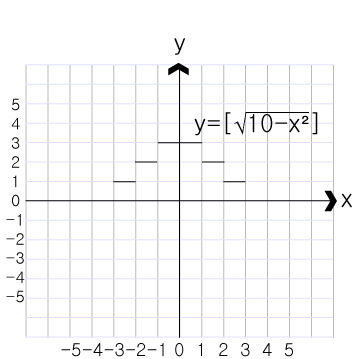
▶x²>10 일때 허수가 되므로 정의역 {-3~3} 의 범위를 지닌다.

▶가우스에 의해 치역은 정수만 지니므로 {3,2,1}의 요소를 지닌다.

 

4)교집합의 갯수 그래프 {집합}

 

xy축이 아닌 ax축입니다.

 

▷A={x|a<x<a+3} B={1,2} 일때 x=n(A∩B)의 그래프 입니다.

▶a<1<a+3 일때 a는 0<1<3 , -1<1<2 에서 0,-1

▶a<2<a+3 일때 a는 0<2<3 , 1<2<4 에서 0, 1

▶x의 갯수는 a=0 일때 2개 a=±1 일때 1개, 그 외의 범위에서 0개

 

5)연립 부등식의 정수의 갯수 그래프

 

 

▷A={(x+3)(x-2)<0} B={(x+1)(x-a)<0} 일때 정수의 갯수 x=n(A∩B)의 그래프 입니다.

▶{-3<x<2}∩{-1<x<a}

▶a=0 에서 정수 0개 , a=1 에서 정수 1개 , a=2 이상에서 2개

 

6)함수 한 밖의 X의 동기화  ※이해필요

▷xƒ(x)=g(x)

▶g(x+h)=(x+h)f(x+h)    ※xf(x) 에 x+h를 대입한게아니라 g(x)에 x+h를 대입한 경우입니다.

 

7)a에 대한 항등식의 정리 ▶이해필요

▷y=x³-ax²+2ax+2

▶x³-y+2-ax(x-2)=0

▶x³-y+2=0=ax(x-2)     ※a에대한 항등식이므로 a=0이 될수 있습니다.

 

8)이차 부등식의 완전제곱식 

▷x²+2x+1+k ≥ 0 , k≥0

▶(x+1)²+k ≥ 0

∴ (x+1)²+k ≥ k

 

9)일차함수와 xƒ(x)의 관계  ※이해필요
▷ax+b=xƒ(x)

∴ƒ(x)=a                 ※ƒ(x)가 x를 품고있다면 x²이 되므로 비성립합니다. b=0, xƒ(x)=ax

 

10)함수 밖의 식의 함수식 ▶어려움

▷ƒ(x) = 이차함수 , ƒ(b)-b²=0 , ƒ(b+1)-(b+1)²=0

▶b와 b+1은 ƒ(x)-x²의 두 근        ※g(x)=ƒ(x)-x²로 판단해봅시다.

▶ƒ(x)-x²의 최대차항 계수는 a-1             ※ƒ(x)=ax²+bx+c라고하면 ax²-x²가 성립합니다.

∴ ƒ(x)-x²=(a-1)(x-b)(x-(b+1))

 

---

수학은 알고 있는 것을 사용할 차례를 발견할 수 있는 능력이 가장 중요합니다.

우리는 그것을 재능이라고 합니다.

만약 그 재능이 없는 사람이 수학을 해야만 한다면 어떻게 해야할까요.

이번 글이. 그에 대한 조금의 답이 되길 바랍니다.