이차함수의 그래프

https://mytory.tistory.com/101

함수와 그래프 (long)

이전에 함수와 그래프에 대해서 다룬 적이 있습니다.

이차함수에 대해서는 함수식에 최대차수가 이차항 이라는것과

이차방정식이므로 인수분해로 근을 구한다는것 외에 추가로 설명할 것이 없습니다.

하므로 이번엔 이차함수보단 그래프 모양에 집중해서 글을 작성했습니다.

---

①그래프의 모양

 

 

이차함수의 근은 2개입니다.

더 큰 해와 더 작은 해를 둘다 표기하면서 그래프의 모양이 양쪽으로 갈라지며

완전제곱식을 만족할때 중근이 되므로 하나의 꼭지점 을 가지게 됩니다.

중근의 밑으로 더이상의 선이 존재하지 않는 이유는 근이 성립하지 않는 구간이기 때문입니다

제곱에서 숫자는 2 , 4 , 8 , 16으로 가파르게 상승하기 때문에 선이 곡선을 띕니다.

 

 

선의 기울기가 클수록 그래프는 더 가파르게 상승합니다.

 

---

②그래프의 이동과 반전

 

1)그래프의 꼭지점

 

 

y = x² + 2x + 2 는 x² + 2x + 1 + 1 이므로

(x+1)² + 1 로 표현할수 있습니다.

혹은 x² + 2x + 2 를 x² + 2x + 1 - 1 + 2 로 변형한뒤에

(x+1)² + 2 - 1 로 계산할 수도 있습니다.

 

+1 은 y축으로 1만큼 평행이동 했다는 뜻입니다.

+1 은 x축으로 -1만큼 평행이동 했다는 뜻입니다.

 

이때 (-1 , 1) 구간은 이차함수 그래프의 꼭지점이 됩니다.

 

y = x² + 2x + 2 라는 이차함수를 예시로 들어서 상수항 2 는 y절편과 일치합니다.

 

x에 0을 대입해보면

y = 0² + 2(0) + 2 = 2

y = (0+1)² + 1 =  2 이므로 같은 값임을 확인할 수 있습니다.

 

만약 x축으로 이동하지 않은 그래프라면 y절편 = 꼭지점 가 성립하겠으나

그외에 y절편 ≠ 꼭지점 임을 주의합시다. 

 

이차함수 그래프는 완전제곱식을 기준으로 하기 때문에 

y = (x+1)(x-1) + 1 과같이 표현된 인수분해된 식에서 상수 1 은 평행이동에 쓰이는 상수항 이라고 볼수 없습니다.

x = 0을 대입하여 y 절편을 구할 수 있으나

꼭지점을 구하기 위해선 식을 풀어서 완전제곱식으로 바꿀 필요가 있습니다.

 

---

y= x² + 2x + 2 에서 x의 절편은 y=0 을 대입하여 x² + 2x + 2 = 0 을 인수분해해서 근으로 값을 얻습니다.

이때 구해지는 값은 근의 성립에 따라서 없을수도 , 1개일수도 , 2개일수도 있습니다.

예를 들어서 x² + 2x + 2 = (x+1)² + 1 이므로 (x+1)² = -1 이라고 하면

이 함수 그래프은 x 절편을 지니고 있지 않습니다.

---

2)그래프의 반전

 

 

이차항이 음수일때 그래프의 상하는 반전됩니다.

반전된 그래프에서도 꼭지점은 (1 , 1) 을 유지합니다.

 

---

3)그래프의 이동

 

 

x축의 평행이동은 이차항에 더한 숫자에 반비례하여 움직입니다.

→인수분해로 근을 구할때 x의 값을 생각해보면 x의 근은 더하는 숫자에 반비례할 것입니다.

y축의 평행이동은 상수항에 비례하여 움직입니다.

 

---

③그래프의 근

 

 

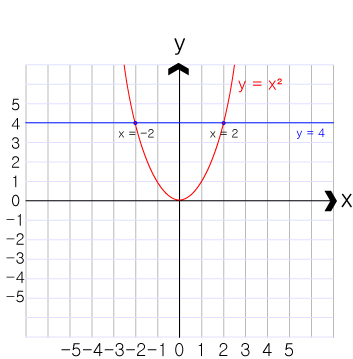
이차함수에서 하나의 y 값에대한 x의 값은 중근과 성립하지 않는 근을 제외하고 2개가 됩니다.

 

 

 

반면 x값에대한 y의 값은 언제나 1개가 됩니다.

 

 

---

이차함수의 그래프 응용은 다음 글에서 이어집니다.