인수분해

---

1.인수분해의 개념

 

①인수분해의 정의

 

 

인수분해란 이차식 이상의 식을 여러개의 일차식이나 숫자로 분해하는 방법 입니다.

이렇게 분리된 일차식 과 숫자 단위를 이용해서 만들어지는 약수 조합들을 인수 라고 합니다.

 

 

 

50 을 소인수분해하면  5 , 5 , 2 의 소인수들이 존재할 것입니다.

소인수들을 조합해서 만들수있는 약수들은 1,2,5,10,25,50 이 있습니다.

마찬가지로 인수도 여러 식과 숫자의 조합을 이뤄낼 수 있습니다.

---

②인수분해 계산하기

 

⑴

 

11x 는 8x + 3x로 바꿀 수 있을 것입니다.

일차항을 임의로 바꿔서 단위별로 식을 정리했을때 같은 식으로 묶인다면

식 (ax+b)를 A 로 치환해서 mA + nA 으로 볼 수도 있을 것입니다.

이때 이것은 (m+n)A 와 같으므로 결론적으로 식을 (m+n)(ax+b)로 분해하게 됩니다.

 

 

⑵

 

위의 식을 ax² + bx + c 라고 표현하고 구하고자 하는 숫자를 m, n 이라고 한다면

m x n = ac , n + m = b 를 만족하는 숫자를 찾습니다.

위의 식을 예를 들어서 4 x 2 = 8 이고, 8은 1x8 과 2x4로 만들수 있습니다.

이때 1 + 8 = 9 이므로 찾고있는 m , n 은 1과 8 입니다.

이를 토대로 x를 8x + x로 표현한뒤에 ⑴ 의 방법으로 인수분해를 진행합니다.

 

 

⑶

 

a와 b의 소인수가 제곱수이며 일차항이 2ab를 만족한다면 위의 공식으로 인수분해를 진행할 수 있습니다.

여기에서 x² 는 x의 제곱이며 계수 1은 1의 제곱이므로 x²도 이에 성립됩니다.

 

이렇게 정리한 식이 자기자신의 곱을 만족할때 그 식을 완전제곱식 이라고 합니다.

 

 

⑷

 

위의 공식에서 중간의 항에 - 부호가 붙으면 정리한 뒤의 괄호안의 부호도 -로 바뀝니다.

-a² + 2ab - b² 은 -(a²-2ab+b²) 으로 바꿀수 있으므로 -(a-b)² 으로 표기할수 있습니다.

 

 

⑸

 

x²+2x-3 이라는 식은 x²+2x+1-4 라고 표현할 수 있습니다.

공식에 따르면 인수는 (x+1+2)(x+1-2)가 나오므로 (x+3)(x-1) 이라고 할 수 있습니다.

 

 

⑹

 

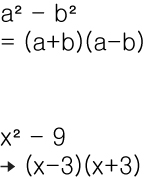
지수가 짝수라면 4차식 이상에서도 적용할수 있습니다.

예를 들어서 x⁴ - y⁸ = (x²-y⁴)(x²+y⁴) 입니다.

 

 

⑺

 

a³ + b³ 에서부터 유도한 정리가 아니라 (a + b)³ 를 변형해서 유도된 공식입니다.

괄호안의 식이 2ab 가 아니라 ab 라는 점에 주의합시다.

 

 

⑻

 

이 또한 괄호안의 식이 2ab 가 아니라 ab 라는 점에 주의합시다.

 

 

⑼

 

괄호 내부에 아직 분리 가능한 수가 남아있지 않는지 꼭 확인합시다.

 

 

⒠역계산하기

 

 

괄호로 묶인 두개의 식 간의 곱셈은 서로간의 모든 항들을 한번씩 곱해줍니다.

(a+b)(c+d) 일때 이 둘을 곱하면 ac + ad + bc + bd 가 됩니다.

항이 3개 이상일때도 모든 항들을 위의 방법으로 곱해서 구합니다.

 

---

2.인수분해의 특징

 

 

이차방정식에서 상수항과 2차항은 서로에게 영향을 주지 않습니다.

역계산에 의하면 상수항은 b와 d 의 영향만 받을것이고 이차항은 a와 c의 영향만 받을 것입니다.

 

---

응용은 다음 글 에서 이어집니다.