-
2.이차방정식 응용수학/중3 2022. 4. 3. 22:06
https://mytory.tistory.com/116
이차방정식
https://mytory.tistory.com/81 일차식 이차식 데이터 처리의 모든 근본 이 돼는 중요한 개념입니다. 특히 데이터의 움직임을 예측하기 위해서 가장 기본적으로 쓰입니다. ① 식의 구성요소와 종류 변수
mytory.tistory.com
이번 글은 이전 글에서 이어집니다.
①중근일 때 미지수 찾기
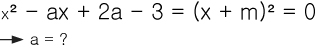

식이 완전제곱식을 만족하려면 일차항은 2AB 를 만족해야합니다. 2AB/2A = B 이므로
이차항과 일차항이 존재한다면 완전 제곱식을 만족하는 상수가 무엇인지 추측할 수 있습니다.
다만 이차방정식은 -2ab 일때도 완전제곱식이 성립되므로
일차항과 상수항이 둘다 미지수라면 값은 두개가 될 것입니다.
②이차방정식과 함수

알수없는 이차방정식인 함수는 f(x) = ax² + bx + c 로 취급합니다.
여기에서 b 나 c는 0일수도 있을 것이므로
실제로는 ax² + bx 혹은 ax² + c 이나 ax²등의 모든 식을 포괄한 표현입니다.
(a가 0이면 이차식이 아니게 되므로 a는 0이 아닙니다.)
함수는 x를 대신에 괄호안의 내용물물로 바꿔서 쓰라는 의미이므로
위에서 정한 가상의 함수에 대입하여
f(x+2) = a(x+2)² + b(x+2) + c 등으로 바꿔서 표현합니다.
위의 식에서 정리가 끝난 2ax + 3a + b=4x-3 는
서로 대응되는 항과 차수를 지니므로 항등식입니다.
f(0) 일땐 모든 x항이 사라지고 상수만 남을 것입니다. 즉 , -1 은 상수항입니다.
그러므로 f(x) = ax²+bx+c² = 2x² -9x -1 입니다.
③넓이와 이차방정식
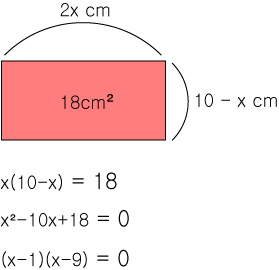
만약에 직사각형 넓이의 가로와 세로의 길이에 같은 미지수 x 가 활용된다면
넓이를 구하는 공식이 이차식이 됩니다.
이렇게 만들어진 식에 대한 넓이를 이미 알고있다면 등식을 통해서 식을 정리 했을때
길이의 근이 2개가 존재한다는 것을 알수 있습니다.
근이 모두 양수라면 둘다 정답이 될수 있겠으나
음수가 있을 땐 길이는 음수의 개념이 존재하지 않으므로 양수인 해가 답이 됩니다.
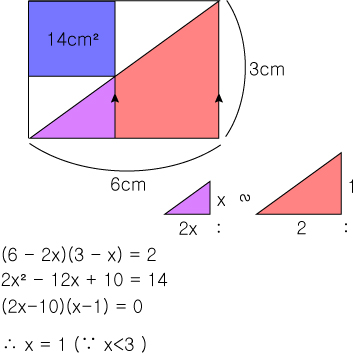
가로와 세로의 길이에 x가 활용되는 예시는 주로 닮음을 통한 미지수 표현이나
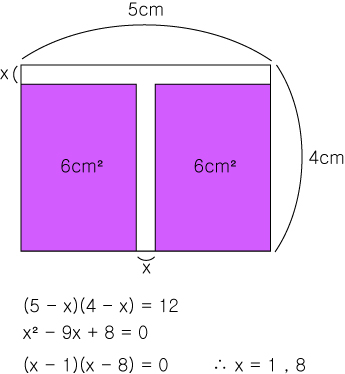
선의 길이를 일부 제거했을때 넓이와 조합해서 볼 수 있습니다.
해설
Q. 가로가 세로보다 3cm 더큰 직사각형의 넓이를 식으로 나타내보세요
→ 가로는 x , 세로는 (x+3) 입니다. 그러므로 넓이의 식은 x(x+3)가 됩니다.
→ 비슷한 예시로 어떤숫자보다 3더 작은 자연수와의 곱 은 x(x-3)이라 나타낼 수 있습니다.
Q2. 로켓이 x초 후에 (20x-5x²)m 지점에 있다면
50m 언덕에서 쏘아올린 로켓이 평지에서 65m 지점에 도달하는건 몇초 후일까요?
→ 시작지점이 50m 혹은 기존에 지닌양이 50개 등등.. 의 기존에 보유한 숫자들은 상수항이 됩니다.
위의 문제를 기존대로 해석해서 20x-5x² = 65 일때 x는? 이라고 본다면
상수값 50이 있으므로 20x-5x²+50 = 65 라고 해석하는 것이 맞을 것입니다.
→ 이차방정식은 이차항이 양수일때를 기본 형태로 봅니다.
위의식은 -5x²+20x-15 = 0 이므로 먼저 5x²-20x+15 = 0 으로 바꿔줄 필요가 있습니다.
→ 이차방정식의 시작시점은 더 작은 양수 혹은 양수 입니다.
이에대한 이해는 이차함수 그래프를 봐야 이해할 수 있습니다.
이차함수는 다음 글에서 다룰 예정입니다.