-
1.부등식의 정의
①부등식의 종류

부등식 : 부등호를 통해서 미지수의 범위를 추정하는 식입니다. 미지수가 없을 땐 부등식이 아닙니다.
일차부등식 : 모든 항의 최대 차수가 1인 식 입니다.
②부등식의 특징
1) 부등식의 변형

부등식 또한 등식처럼 식의 변형이 가능합니다.
2) 두 부등식을 합산

두개 이상의 부등식을 합쳐서 합쳐진 식으로 압축할 수 있습니다.
3) 부등호의 반전
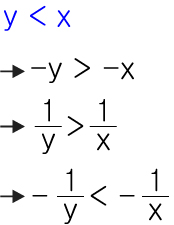
부등호는 양변의 식이 음수가되거나 분수식이 될때 위치가 반전됩니다. (3 > 2 이므로 -3 < -2)
4) 부등식의 해

부등식은 등식과 달리 해가 여러개가 존재할 수 있습니다.
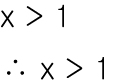
그중에서도 최대치 혹은 최소치가 존재하지 않을 경우 부등식 자체를 해로 사용하기도 합니다.
2.부등호의 응용
①분배법칙으로 부등식 정리하기

분배법칙을 적용해서 나온 분리된 요소를 양쪽 변에 나눠서 수를 정리할 수 있습니다.
②소수가 쓰인 부등식 정리하기
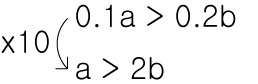
부등식에 유한소수가 쓰여있다면 다른 변에 10의 단위로 같이 곱을 해서 정수로 표현할 수 있습니다.
③두개의 부등식을 비교하기
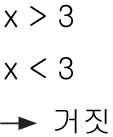
한개의 미지수에 대해서 정리가 끝난 두개의 부등식을 비교해봤을 때
둘을 모두 만족하는 해를 찾을수 없다면 이 식중에 하나 혹은 둘은 거짓 일 것입니다.
④등식과 부등식을 비교하기

부등식 내용의 일부중에 등식을 구한 내용이 있다면 이를 적용해볼수 있습니다.
b + d = a + c 이므로 a + b + d = a + a + c 로 바꿀수 있을 것입니다.
그리고 b + a + c < a + a + c 가 되므로 양면에 a 와 c를 빼서 b < a 라는 결과를 얻을 수 있을 것입니다.
⑤부등식과 좌표평면
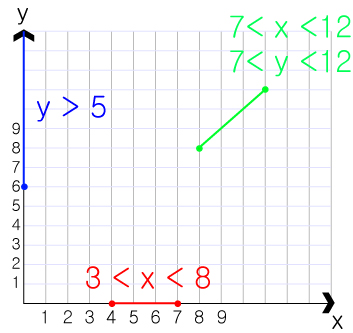
좌표평면에서 부등호의 양쪽 변 중에 값이 큰변은 선의 끝점을, 작은변은 시작점을 가리키게 됩니다.
이는 부등식이 직선의 시작/끝 점을 지정하거나 선분을 그을 때 쓰인다는 의미로 볼수 있습니다.
ex.수학 외의 기타 사항
부등식 부터 서서히 문제에서 식을 스스로 찾으라는 과정이 늘어나기 시작합니다.
문제들 속에서 식을 추출하는 과정이 제각기 다르므로 모든 예제를 볼수는 없겠지만
하나의 문제를 보면서 대략적으로 식을 추측해보는 단원을 마련해봤습니다.
Q. 반지름이 4cm인 원기둥의 넓이를 30m³ 이하로 만들때 높이 Am 가 가질 수 있는 정수의 해를 모두 더한 값은?
point 1. 현재 배우고있는 과목을 먼저 파악해봅시다.
문제를 무슨 식으로 어떻게 바꾸라는것인지 안보인다면 현재 무엇을 배우고 있는지 생각해봅시다.
지금 배우고 있는것은 부등식 이며 우리는 기둥의 넓이를 배우고 있는 것이 아닙니다.
그러니까 이 문제에서 추출해내야 하는 최종적인 식은 부등식일 것입니다.
point 2. 적혀져있는 것들은 일단 전부 그려보거나 나열해 봅시다.
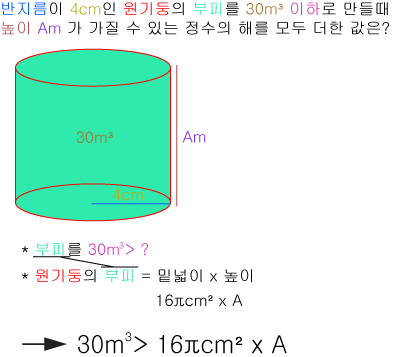
그림으로 그려야 돼는 정보들을 억지로 글에 쑤셔넣은 문제들이 생각보다 많습니다.
그래서 설명하는게 그림이라면 일단 그려봤을때 풀이의 방향이 보이는 경우가 꽤 많습니다.
어떤 풀이도 보이지 않는다면 글자의 은/는/이/가 를 모두 제거하고 명사만 남겨봅시다.
혹은 이전에 배운 공식들이 보인다면 일단 적어본뒤에 문제안에 있는 숫자들을 넣어봅시다.
point 3. 언제나 단위 표기에 주의해야합니다.
1m 는 100cm 입니다. 그런데, 1m² = 100cm x 100cm = 10000 cm² 입니다.
그러니까 16πcm² ≠ 0.16πm² 이며 0.0016πm² 라고 적어야 맞습니다.
비슷한 유형으로 1시간은 100분이아니라 60분이라는점을 이용하기도 합니다.
point 4. 문제의 마지막을 잘 살펴봅시다.
값을 구해보면 높이 A는 π를 3.14로 취급하여 나누었을때 약 5,971.337 m > A 가 되어야 하는 것을 볼수 있습니다.
문제에서는 정수의 합 이라했습니다. 즉, 소숫점 단위는 에초에 구할 필요가 없다는 소리입니다.
높이 0 에선 원기둥이 성립할수 없고 정수 라고 했으므로
1≤x≤5971 의 값을 모두 더하면 답이 될 것입니다.
*문제 풀이에 대한 해석을 설명하는 것이 목적이기 때문에 답을 구하는 것은 주제를 벗어납니다.
*만약 답이 궁금하다면 1~5971 까지 숫자의 덧셈을 쉽게하는 구하는 방법을 스스로 찾아봅시다.
*힌트는 중앙값입니다.
'수학 > 중2' 카테고리의 다른 글
함수와 그래프 (long) (0) 2022.03.21 연립방정식 (0) 2022.03.16 중2과정에서 배우는 기타 항목(short) (0) 2022.03.14 제곱의 정리(long) (0) 2022.03.14 유한소수 무한소수 (short) (0) 2022.03.14