[수열] 항의 합수열과 멱급수

 

글의 제목에서는 항의 합수열이라고 작성했으나 수학적으로 옳은 명칭이 아닙니다.

마치 부등호에따라 기울기가 변하는 (조건함수) 처럼 정해져있는 명칭이 없습니다.

 

정규과목에서는 수열의 합 이라고 명칭하여 설명되고 있으나

그것이 의미하는 것이 {An} + {Bn} 인지

아니면 {An} 내부의 모든 항들의 합인지 구분이 안돼서

작자는 항의 합수열(줄여서 항의합)이라 부릅니다.

 

만약 반복되는 실수의 합을 찾는다면 기타 과목을 참고해주세요

 

---

1.개념

 

[항의 합]

 

1.항의 합집합의 정의

 

 

수열이 지니고 있는 각자의 순서까지의 모든 항의 합을 모아서 새롭게 수열을 이뤘습니다.

이때 이 수열은 S로 작성하며 , S₃=6 으로 각자의 항을 지니고 있습니다.

 

---

2.일반수열에서 항의 합 불러오기

 

①등차수열 에서 불러오기

 

 

모든 등차수열의 합은 첫째 항 α 와 지정한 끝항 ω 의 합에 ÷2 를 한것과 같습니다.

위의 식은 이를 정리한 것입니다.

 

②등비수열 에서 불러오기

 

 

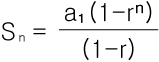
등비수열의 합은 S-rS 를 S(1-r)로 묶어서 분모로 보냈기 때문에 위의 형태가 나옵니다.

 

본래라면 분모분자에서 1>r 일때 1-r , r>1 일때 r-1 로 바꿔서 써야됍니다.

차라리 그렇다면 , 작자는 두개의 (1-r) 부분을 |1-r| 로 외우는 것을 추천합니다.

 

---

3.항의 합의 성칠

※입력의 한계로 첨자를 주황색으로 표시했습니다.

 

①S₁=a₁

②Sn-Sn₋₁=an

④S₄-S₂ = a₄+a₃

 

3-2.등차 항의합 의 성질

 

S = An²+Bn+C 일때 등차수열을 만족합니다.

⑴공차는 2A가 됩니다.

⑵C≠0 일때 2항부터 등차수열입니다.

⑶항 사이의 폭(기울기)이 점점 크게 오르므로 그래프상에서 이차함수가 됩니다.

⑷그래프 모양은 1사분면의 정수마다의 점선이 됩니다.

※만약 수열 사이를 무한히 소수단위로 분리하면 공차,공비의 개념이 사라지며 일반적인 실수가 됩니다.

 

3-3.등비 항의합 의 성질

 

S = Arⁿ+B (r≠1,0) 이며 A+B=0일때 등비합을 만족함, 

⑴A+B=0을 만족해야 하는 이유는 식정리에 의한 이유입니다.

→ a₁(1-rⁿ)/(1-r) = {a/(r-1)}rⁿ-{a/(r-1)}  ∴ (A = B = a/(r-1))

⑵r-1 을 지니므로 r=1일때 분모 0에 의한 성립불가 , r=0일때 상수함수가 됩니다. 

⑶그래프는 지수함수가 됩니다.

⑷그래프 모양은 1사분면의 정수마다의 점선이 됩니다.

 

---

[멱급수]

 

1.정의 : (등차수열 x 등비수열) 의 항을 지니는 수열입니다. 
ex) S = 1·½ + 2·½² …

 

2.멱급수의 성질과 변형 {이해력 다소 필요}

 

1)r합차 성질

S - rS = 1·½ + (2·½² - 1·½²) …  + n·½ⁿ⁺¹    (∵ r=½)

S-½S 와 같으므로 S-½S=½S 

이때 ½S = ½ + ½² … + n·½ⁿ⁺¹ 로 정리됩니다.

 

2)수열 × 실수

½S ÷ ½ = S = 1(½÷½)+½+½²...n·½ⁿ = {등비수열의 합} + n·½ⁿ

 

---

2.응용

 

[추가 지식]

※몇 구간에서 첨자를 주황 글씨로 표기했습니다.

 

1.S₀와 이차식의 상수항 C {가상 개념}

 

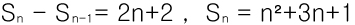
n=1 을 대입하면 S₁=a₁=5 , S₁-S₀=4
여기에서 S₁-S₀ ≠ a₁ 이므로 An는 두번째 항부터 등차를 이룬다고 할 수 있습니다.

S₀은 n=0을 대입한 상수항에 해당하기 때문입니다.

 

등비항의합에서 이 개념을 적용한다면 n=0 에서 Arⁿ+B가 A-B가 되므로

결과값이 0이 아닐때 등비합이 아니다 라고 결론 지을 수 있습니다.

 

2.S=ƒ(x)식에서의 x의 제한

Sn=3xⁿ-2
x=0,1일때 Sn은 상수함수가 되어 버리므로 수열이 성립하지 않습니다.

그러므로 x≠0,1 이 됩니다.

 

※수열이 {-1,0,1}의 대칭형일때 Sn=상수 가 나올수는 있습니다.

그러나 위의 식에 의하면 S₁=3x¹-2 가 되어 x=1일때 모든 항이 1이 됩니다.

그래서 성립할 수 없는 것입니다.

 

3.Sn의 부등식으로 음수의 시작점 찾기

Sn= -n(2n-52) 라고 가정합니다.

음수를 만족하는 n을 찾으므로 식에 <0의 부등호를 붙혀서 판단합니다.

-n(2n-52)<0 (Sn<0) → n(2n-52)>0 (∵n>0)
이때 n<0 , n>26 라고 하면 n>26 에서 n이 27이상일때 Sn<0가 만족합니다.

 

4.부분수열
짝수 항만 모아서 a₂=6,a₄=10,a₆=14 라고 할때

a₂n=a2,a4,a6…a2n

그리고 이 부분수열만으로 항의합수열을 구성하면

Sn=a2+a4+a6…a2n

그러면 이때 S₁=6, S₂=16

즉 , 항의 합수열을 통해서 수열에서 일부분만 추려낸 변형 수열을 구성할 수 있습니다.
짝수 항이아닌 홀수항인 a₁,a₃,a₅ 등의 여러 변형 방법이 존재합니다.

 

5.홀수항의 갯수
1~101까지 항중에서 홀수 항의 갯수는 2n-1=101 에서 n=51

 

---

[테크닉]

※몇 구간에서 첨자를 주황 글씨로 표기했습니다.

 

①

a(1+2+3+4) + a(n-0+n-1+n-2+n-3) = 160
>4(a₁+an)=160 
∴ a₁+an=40

 

※+는 a₁+a₂를 의미합니다.

 

②

a₁+a₂=96 , a₁+a₂+a₃+a₄=120
→ s₃+s₄=24 (등차중항과 맞지 않으므로 등비수열 혹은 그외)

→ r²(a+ar)=24
∴ 96r²=24 (∵ a+ar=a₁+a₂)

 

③

S₃ = 7 , S₆ = 63

→S₆ = a(r⁶-1)/r-1

→a(r³-1)(r³+1)/r-1
∴ S₃(r³+1)=63

 

④

{2+½,4+¼,6+⅛}

= {(2+4+6) + (½+¼+⅛)}

= Sn+S'n