-
1.직선의 방정식
①직선의 표현
1)직선 L
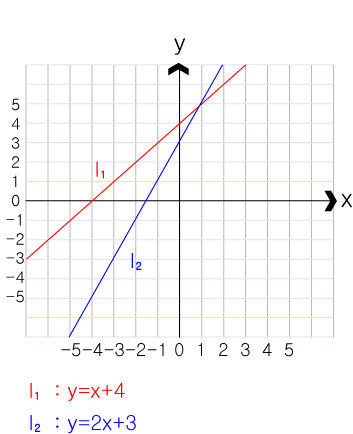
직선은 방정식 을 공개하지 않고 l₁,l₂ 로 작성하여 간단하게 표기할 수 도 있습니다.
반대로 방정식마다 개인의 이름을 붙힐때 l₁ : y=ax+b 의 형식을 사용하기도 합니다.
2)직선위의 임의의 점
y=x+1 의 방정식이 y값이 a인 지점을 지나간다면 x의 값은 a+1 이라할 수 있으며
순서쌍으로 나타내면 (a+1,a)가 됩니다.
반대로 x의 값이 a라고한다면 (a,a-1)이 될 것입니다.
x-y+1=0 위의 임의의 점을 (m,n) 이라고한다면
항상 m-n+1=0 이 성립합니다.
②직선의 방정식
⑴개념

우리는 앞서 중2과정에서 2개의 점으로 직선의 방정식을 구하는 방법을 배운 적이 있습니다.
점이 1개만 제공되어있는 직선의 방정식도 어느정도 추정 할수 있는데 이를 직선의 방정식이라 합니다.
즉, 기울기를 알수없는 직선이 점 (m,n) 을 지날때 y-n=a(x-m)의 형태를 띈다고 할 수 있습니다.
이때 y-n=a(x-m) 형태를 지니는 방정식을 일반형
ax+by+c=0 의 형태를 지니는 방정식을 표준형 이라고 합니다.
y에 대한 정리는 함수식이라 합니다.
⑵기울기

만약 기울기가 내려가는 모습이라면 기울기 a의 값은 음수가 될 것입니다.
이를 -a 라고 작성할 경우 a자체는 양수가 되어야 한다는 것을 주의해야합니다.
쉽게 말해서 -(3) 을 -(-3)으로 쓰지 않게 주의하라는 의미입니다.
원한다면 부호 -를 제거하고 똑같이 a로 작성해서 쓸수도 있습니다.
⑶직선의 중심

(m,n) 은 직선이 기울기 a에 상관없이 반드시 지나가게되는 직선의 중심이라고 할수 있습니다.
y=x+1 일때 이 직선은 기울기 상관없이 반드시 y-0=x+1 에따라 (-1,0)좌표에 중심점을 지닙니다.
⑷원점을 지나는 직선

직선이 원점을 지난다면 기울기 a 의 값은 직선의 중심을 (x,y)라고 할때 y/x가 됩니다.
③x/a+y/b=1

x절편을 a , y절편을 b, 직선위의 임의의 한 지점을 (x,y)라고 한다면
x/a+y/b=1가 항상 성립합니다.
2.두 직선의 관계
l₁ : y=ax+b l₂ : y=mx+n l₁ : ax+by+c=0 l₂ : mx+ny+k=0 교점을 지닌다.
한점에서 만난다.a≠m a/m ≠ b/n 평행하다.
근이없다.a=m, b≠n a/m = b/n ≠ c/k 일치한다.
근이 무수히 많다.a=m, b=n b/n = c/l 수직이다. a×m=-1 am+bn=0
3.직선과 점의 거리
1)점

점과 직선 사이의 거리란 점에서 직선을 향해 수선의 발을 내렸을때 그 좌표와의 유클리드 거리를 의미합니다.
계산 과정을 정리한 간단한 식을 사용합니다.
공식을 사용할 경우 분모의 근호는 x1을 해서 분자로 올려줍니다. (ex. 1/√2 × √2/√2 = √2/2)
계산 과정을 알아둘 필요가 있습니다.
- (m,n)에 대한 직선의 방정식을 구합니다.
- l₁ : ax+by+c 에 수직인 기울기를 구합니다. (a를 -1로 만드는 숫자를 구합니다.)
- 직선에 방정식에 구한 기울기를 적용합니다. (l₂)
- l₁ 과 l₂ 의 연립방정식을 통해서 교점을 구합니다.
- 교점과 점 (m,n) 사이의 유클리드 거리를 구합니다.
직선과 직선의 거리에 응용할 경우 직선 l₂위의 임의의 점 하나와 의 거리를 측정합니다.
2)선분
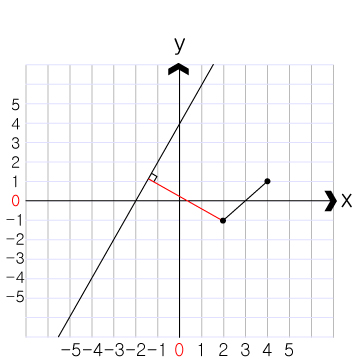
직선과 선분의 거리일 경우 선분의 시작점과 끝점중에서 더 가까운 쪽의 점과의 거리를 측정합니다.
3)최대거리

기울기 a가 정해져있지 않은 직선의 방정식과 임의의 점의 거리는
수선의 발이 서로 수직할때 최대 거리를 지닙니다.
4.직선과 직선의 교점의 범위

만약 직선의 방정식이 직선 l 와 1사분면에서 만나고자 한다면
이때 교점은 x를 기준으로 x절편>x>y절편의 범위를 지니게 됩니다.
2사분면에서 만나고자한다면 x<y절편이며 기울기 a가 직선 l 과 평행하지 않은 범위를 지닙니다.
3사분면에서 만나고자한다면 x>x절편이며 기울기 a가 직선 l 과 평행하지 않은 범위를 지닙니다.
4.응용
A1)

A2)

기울기 a 가 -1 이라면 두 방정식은 각각 x+y=0 , x+y+3=0 이 되므로
A=1 , B=1, C=3이 될 것입니다.
물론 거리가 같은 다른 경로인 a= -23/89 일때의 해도 존재합니다.
다만, 이 경우 두 직선의 방정식이 C의값이 각각 존재하게 될 것입니다.
A3)

삼각형의 넓이를 구할때 직선과 점의 거리가 응용됩니다. A4)

만약 각도가 주어졌다면 피타고라스의 정리 외에 cos θ를 활용할 수도 있습니다.
5.심화
a)super hard

임의의 점 하나와 직선 위의 모든 점들 사이의 중점들을 모으면 그림과 같을것입니다.

모든 점들의 자취들을 따라서 선을 그으면 원본의 직선이 중점만큼 움직인 모양의 직선이 됩니다.
이때 이 직선을 방정식으로 나타낸다면 이것을 자취의 방정식이라고 합니다.
중점의 자취의 방정식을 구하는 방법은 다음과 같습니다.
직선을 ax+by+c
임의로 찍은 저 빨간점의 좌표를 (n,m)
빨간점과 직선의 중점들을 (x',y')
직선위의 임의의 점을 P(x) 라 해본다면 이때
x' = m+P(x)/2 입니다.
그리고 이를 정리하면 m=2x'-P(x) , n=2y'-P(y)
여기에서 자취의 방정식은 an+bm+c가 되며
즉 a(2x'-P(x))+b(2y'-P(y))+c 가 자취의 방정식이 됩니다.
식을 정리한 뒤엔 x',y' 를 x,y로 바꿔 작성해줍니다.
b)

두 직선의 끼인각을 2등분하는 빨간직선위의 점을 P(x,y)라고 하고
양쪽 파란 직선 두개를 각각 l₁, l₂ 라고 해봅시다.
이때 P와l₁, P와l₂ 사이의 거리는 같을 것입니다.
두 거리의 공식을 등식으로 묶어서 정리하면

이 식을 정리하면 결과로 빨간 직선의 방정식이 나오게 됩니다.