피타고라스의 정리

---

1.유클리드의 증명

 

 

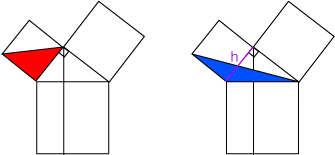
위의 사각형들은 모두 정사각형이라고 가정합니다.

빨간 삼각형과 파란 삼각형은 높이와 밑변이 같으므로 같은 넓이일 것입니다.

 

 

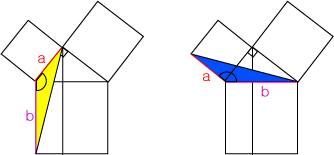
파란 삼각형와 노란 삼각형은 SAS합동이므로 넓이가 같을 것입니다.

 

 

노란 삼각형과 초록 삼각형은 높이와 밑변이 같으므로 같은 넓이일 것입니다.

 

 

그러므로 빨간 삼각형과 초록 삼각형은 같은 넓이입니다.

 

 

즉 빨간 사각형과 초록 사각형은 서로 같은 넓이일 것이며,

반대편의 파란 사각형과 노란 사각형은 서로 같은 넓이 일 것입니다.

 

 

초록 사각형과 노란 사각형을 합친 넓이를 청록 사각형이라고 한다면

빨간 사각형 + 파란 사각형 = 청록 사각형이 될 것입니다.

 

 

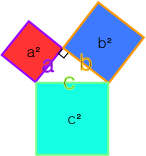
사용된 정사각형들의 넓이는 변의 길이의 제곱이 될 것입니다.

즉 , 직각삼각형을 구성하는 변들은 a² + b² = c² 를 만족합니다.

이 a² + b² = c² 를 피타고라스의 정리 라고 합니다.

 

유클리드 증명은 피타고라스의 정리를 증명하는 수많은 예시중 하나입니다.

 

---

2.피타고라스의 정리 응용

 

①직각삼각형 파악하기

 

 

역으로 말해서 만약 삼각형의 변의 길이가 a² + b² = c² 를 만족한다면

그 삼각형은 직각삼각형 일 것입니다. 

 

---

②예각삼각형의 기준

 

 

a² + b² = c²를 만족하면 직각삼각형이므로

예각 삼각형을 그릴때 B변의 길이를 위 공식에 만족하지 못하게끔 제한할 수도 있을 것입니다.

 

---

③유클리드 도형의 넓이

 

 

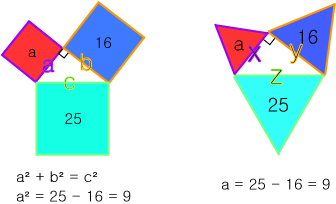
유클리드 예시 도형에서 정사각형의 넓이가 주어져있을 때 

정사각형의 넓이는 변 a 의 제곱이므로 a² + b² = c²를 그대로 응용할 수 있습니다.

위의 예시에서 빨간 사각형의 넓이는 청록 사각형 - 노란 사각형인 9cm² 일 것입니다.

 

마찬가지로 닮은 도형들의 대응되는 변으로 직각 삼각형을 만들수있다면

이 공식을 그대로 적용해서 넓이를 구할 수 있습니다.