-
항등식 추정과 내림차순수학/고1 2022. 5. 28. 23:23
본론으로 들어가기 앞서서 필요한 보조 개념 몇 가지만 살펴봅시다.
항등식 : 식에 들어있는 미지수 a가 어떤 숫자가 되어도 항상 성립하는 등식
내림차순 : 큰 숫자(혹은 개념) 에서 작은 숫자 순서대로 배열한 것 (ex.5 4 3 2 1)
오름차순 : 작은 숫자(개념)에서 큰 숫자 순서대로 배열한 것(ex. 1 2 3 4 5)
항등식은 내림차순으로 정리한 상태를 기본으로 시작하기 때문에 내림차순과 필연적으로 엮여있습니다.
1.k에 대한 내림차순
1) x에 대한 내림차순

x에대한 항등식을 구하라고 한다면 가장 먼저 x를 기준으로 내림차순 정리해 주고 시작합니다.
2) x,y에 대한 내림차순

x,y에 대한 항등식(즉, x값과 y값이 어떤 값이여도 항상 식이 참이되는경우)를 구하라고하면
차수 를 기준으로 정리합니다.
그 중에서도 미지수의 알파벳이나 공학기호등의 순서에 따라서 우선순위를 지닙니다.(x>y , a>b)
3) x 혹은 y에 대한 내림차순

x와 y 둘다 2) 처럼 항등식이 성립하지만, 그 중에서 하나를 지정해야한다면
최대 지수가 낮은 미지수를 기준으로 정리합니다.
만약 두 미지수의 최대 지수가 같다면 순서에 따라 우선순위를 지닌 미지수를 기준으로 합니다.
2.미정계수법
식에 적혀있는 항등식 외의 미지수를 추측하는 방법입니다.
1) 계수비교법
항등식일 때만 성립합니다.
내림차순으로 정리하게돼는 이유입니다.
⑴ 기본개념

⑵ 영등식의 항등식

⑶ ax²+bx=c

x값에 상관없이 항상 성립하기 위한 경우의수는 0 이외에 존재하지 않습니다.
- ⑶ 주의할점

인수분해 되어있는 식에 대해선 ax²+bx=c 가 성립할 수 없습니다.
또한 인수분해 되어있는 식에 대해서 계수비교법은 사용할 수 없습니다.
2)수치대입법
x값이 어떤 값이여도 상관 없으므로 원하는 임의값을 대입해서 미지수를 알아냅니다.

3.응용
아래의 예제들은 x값에 대한 항등식이라는 전제로 진행합니다.
A1)

A2)
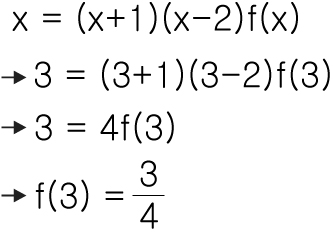
A3)
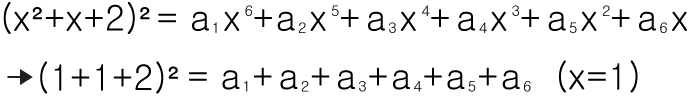
A4)
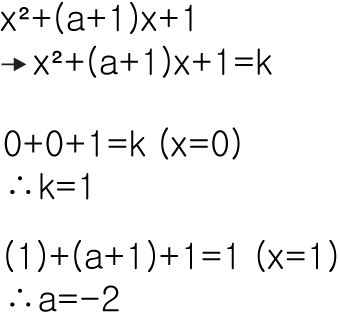
'수학 > 고1' 카테고리의 다른 글
허수와 복소수 (0) 2022.05.29 함수의 나눗셈 (0) 2022.05.29 인수분해(응용과 심화) (0) 2022.05.28 인수분해(지수3의 공식과 여러가지 분해과정) (0) 2022.05.28 다항식의 곱과 나눗셈 (0) 2022.05.26
