인수분해(응용과 심화)

이전 글에서 이어지는 내용입니다.

---

 

1.응용

 

A1)

 

A2)

식 전개에 쓰입니다.

 

A3)

가장 많이 나오는 유형입니다.

 

---

2.해설

 

A1)

원기둥의 높이가 반지름보다 2cm 크다면 넓이는?

>h(높이)=(x+1), r(반지름)=(x-1) → S(넓이) = (x+1)(x-1)²π

 

A2)

x⁴+ax³+2x+1 이 (x-1)을 인수로 지니고 있을 때 a값은?

>x⁴+ax³+2x+1 ÷ x-1 을 조립제법으로 진행하고 나머지가 0이 되는 a값을 구합니다.

 

---

3.심화개념

 

작성자가 직접 고안한 문제들이 아니며, 실제로 문제풀이에 존재하는 것들입니다.

누군가가 알려주기 전까진 스스로 해법을 찾기 매우 힘든 문제들을 예시로 보여드립니다.

 

a)Super Hard

이해하기보단 결과를 구하기 위한 용도로써 과정을 외우는 것을 추천합니다.

 

b)

 

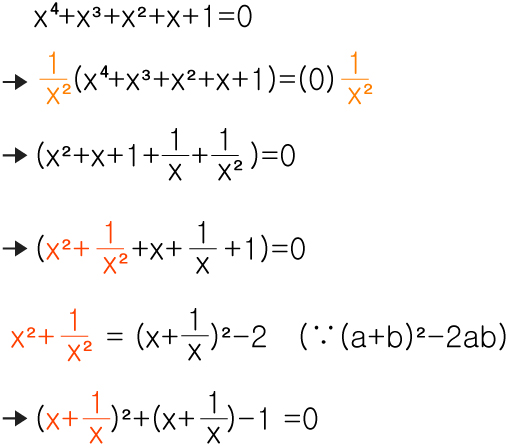
c)

 

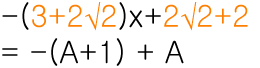
d)

 

즉, 미지수가 있는 이차방정식에 임의의 원하는 값을 대입하면

이때 a의 값은 대입한 값이 근으로 존재하게하는 값으로 변형됩니다.

 

e)

Q1.

f(x) = x²+(a²-3a-4)x-a+2 가 완전제곱수가 되기 위한 조건은? 

>a²-3a-4 = 2(2-a) 

 

Q2.

f(x)가 (x-m)(x+m)를 만족하기위한 조건은?

>a²-3a-4 = 0 , (-a+2)가 음수여야되므로 a>2