약분과 분수의 곱셈

https://mytory.tistory.com/29?category=987786 

분수와 크기 비교

 

우리는 앞서서 분수에대해서 설명할때 잠깐 약분의 개념이 무엇인지 설명했던 적이 있습니다.

 

https://mytory.tistory.com/47

약수와 배수

 

또한 우리는 전에 최대공약수가 무엇인지 배웠고, 그것을 어떻게 활용하는지 설명했었습니다.

이번엔 이 최대공약수의 개념을 이용하여 분수를 약분하는 과정을 살펴보고

이를 이용한 분수들의 곱셈을 진행할 것입니다.

---

https://mytory.tistory.com/30?category=987786 

 

만약에 곱셈 중에 대분수를 가분수로 바꾸는 법을 잘 모르겠다면 이 글을 참고하시면 됩니다.

 

https://mytory.tistory.com/48

 

분수의 종류마다의 이름은 이전 글에 써 놓았습니다.

---

1.약분을 해보자(1/2)

 

분수의 분자와 분모를 최대공약수로 나누면 많은 분수들을 약분할 수 있습니다.

이때 이렇게 약분을 끝낸 분수를 기약분수 라고 합니다.

 

다만, 이번에 우리가 구할 것은 최대공약수가 몇인가? 가

아니라 분수를 약분하는 것 이므로

우리는 최대공약수를 구하는 과정을 응용해서 기약분수를 더 쉽게 구해볼 것입니다.

 

 

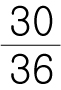
30/36 을 약분 한다고 하면,

 

 

일단 3으로 나누어 떨어질 것 같으니 먼저 3으로 나눠봅시다.

 

 

그리고 2로 나누어 떨어질것 같으니 2로 나눠봅시다.

그리고 그렇게 나온 기약분수는 5/6 이라는 것을 알 수 있습니다.

 

물론 최대공약수인 6으로 바로 나누어도 같은 결과를 얻을 수 있습니다. 

다만 숫자가 클 경우에는 이렇게 진행하는 방법이 있다는 것을 보여드리기 위해서 설명드렸습니다.

 

---

2.분수의 곱하기(1/2)

 

 

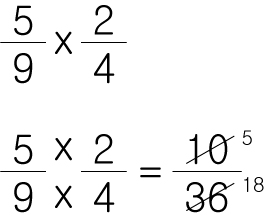
분수끼리 곱할때는

분자 x 분자 / 분모 x 분모 를 하면 됩니다.

 

이해를 해봅시다.

분자 = 원래 소유하고 있는 숫자

분모 = 거기에서 나눌 숫자 라고 생각해봅시다.

 

그렇게 생각하고 5 ÷ 5 x 5 ÷ 5 를 바라봅시다.

가지고있던 5 에다가 5 을 나누고 5를 한번더 나눈뒤에, 5를 곱하나

5에다가 미리 5를 곱한뒤에 5하고 5로 나누나 결국 결과는 똑같겠죠?

 

그래서 분자끼리 먼저 곱해준 다음에 분모로 두번 나누는 작업을 하는 것이 원리라고 생각하면 됍니다.

물론 이때 , 16 ÷ 4 ÷ 4 는 16 ÷ (4 x 4) 와 같겠지요. 그래서 분모도 분모끼리 곱하는 것 입니다.

 

 

그리고 나온 결과값은 기약분수로 만들어서 보기 편하게 해줍시다.

 

 

물론 곱셈을 하기 전에 미리 약분을 해도 같은 결과를 얻을 수 있습니다.

1/2(1÷2) 이나 2/4(2÷4) 이나 둘다 똑같을 테니까요.

---

1-2.약분의 특징(2/2)

 

곱하기는 9 x 4 를해도 4 x 9 를 해도 똑같은 결과가 나온다는 것은 이미 아실 겁니다.

그런데, 그렇다는 말은 

 

 

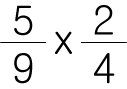
이런 상황이 아니라,

 

 

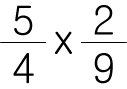
이런 상황이 나타나도 결과는 똑같다는 소리겠죠? 그렇다면,

 

 

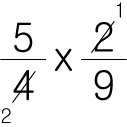
결국 이렇게 약분하는 것이 가능하다는 것입니다. 잘 숙지해둡시다.

---

2-2.대분수와 가분수를 곱하기(2/2)

 

 

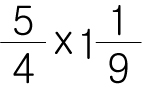
가분수는 가분수인체로 곱하면 됩니다.

하지만 대분수는 대분수인 상태 그대로 곱하는 방법이 존재하지 않습니다.

 

 

하므로 대분수는 가분수로 바꿔서 계산해줍니다.

이 과정에서 더 간편한 계산을 위해서 약분도 해줍시다.