-
몇 배인지 가늠하기와 공간지각능력
초등학교 고학년 단위로 올라왔기 때문에 앞으로의 글은 곱셈, 덧셈, 뺄셈를 할 수 있고 크기 단위를 읽을 수 있다는 전제하에 쓰겠습니다. 초등학교 4학년 과정에서는 수학과 동시에 '공간지각
mytory.tistory.com
이 글은 이전 글에서 이어집니다.
이번 내용이 수학의 두번째 고비입니다.
약수는 계산을 하면서 일정 수준이 지나면 11, 13, 17, ... 일일히 대입해가면서 알아가야 합니다.
그런식으로 숫자를 대입하면서 일일히 약수를 구하는 것은 사람이 하기엔 매우 힘든 과정입니다.
약수 구하기는 보통 컴퓨터에게 시켜야 맞는 작업입니다.
그래서 사람이 푸는 문제 풀이에서 사용되는 숫자들은 약수가 작은 숫자들만 주로 사용될것 입니다.
여기에선 이해를 위해서 큰 숫자를 약수로 나눠보고 약수의 개념을 이해할 것 입니다.
그 후, 반대 개념인 배수에 대해서 알아 볼 것입니다.
1.약수의 개념(1/3)
약수를 비유하자면 시계를 구성하고 있는 작은 부품들이 무엇이 있는지 알아내는 과정입니다.
이중에서 빼도 돼는 부품이 있다면 빼서 계산을 할때 숫자의 크기를 줄이는 용으로 사용됩니다.
색으로 다시 비유를 하자면,
빨간색과 파란색을 합치면 보라색이 돼니까 보라색의 약수는 빨간색 과 파란색 입니다.
이제 이것을 숫자에 비유해 봅시다.
35 라는 숫자를 예시로 쓰자면 7 x 5 = 35 이고 35 x 1 = 35 니까
35 라는 숫자를 만들기 위해서 사용되는 숫자는 1 , 5 , 7 , 35 가 돼겠군요.
정리하자면 약수란 , 큰 숫자가 어떤 작은 숫자들로 구성되어 있는지 그 목록 이라고 할 수 있겠습니다.
약수의 조건은 두가지 입니다.
- 숫자를 오직 곱하기로만 만들 때의 필요한 작은 숫자들
- 만약에 약수를 구했는데 똑같은 숫자들이 나온다면 그중에 하나만 취급할 것
▷2번째 조건의 이유
시계가 있을 때 우리는 이것이 어떤 부품들로 이루어 졌는지 궁금할 뿐,
그중에서 똑같은 부품들은 또 총 몇개 씩 있는지 알려고 한 것은 아닙니다.

이것은 마치 이 그림에 있는 색의 종류는 총 몇가지인가요? 라고 질문 했을 때
빨간색 8개 파란색 7개 노란색 6개 있어요 라고 안하고
3가지 종류가 있습니다 라고 말하는 이유와 같습니다.
이제 약수의 개념을 그림을 보면서 조금더 깊히 이해해 봅시다.

금구슬 20개가 있습니다. 구슬 20 개를 작은 단위 갯수만큼 정리해서 놓는다고 했을 때
4 X 5 = 20 이니까 4와 5 라는 약수가 나옵니다.
그런데 이것을 다시 생각해 본다면 이것이 20을 구성하는 가장 작은 단위의 정리라고 할 수 있을 까요?
그러면 이렇게 보는건 어떨까요?

4또한 2 x 2 와 4x1 로 구성 되어있으니 이것을 약수로 분리해 주는 겁니다.
즉 , 20이라는 숫자를 가로와 세로만 놓았을때, 비는 공간이 없게 배치하기 위해선
1 , 2 , 4 와 5 , 20 이라는 숫자를 사용할 수 있다 라고 생각할 수 있습니다.
이때 4 x 5 로 쓰면 돼는 것을 왜 4를 2x2 로 분리하는 가 에 대한 의문이 있을 수 있습니다.
이해를 돕기 위해서 비유해서 설명하자면 그 말은, 총 512 장의 종이로 구성되어 있는 책이 있는데
그 중에서 종이 2장이 풀로 딱붙어있어서 512 장을 511장이라고 부르고 있는것은 아닐까요?
그래서 약수는 나눌 수 없는 가장 작은 숫자들을 포함해서 구성하는 것 입니다.
약수를 구해보자(2/3)
약수를 구하기 앞서 기본적으로 알아야 돼는 것들을 설명하겠습니다.
- 10 이상의 0 으로 끝나는 숫자는 2와 5로 나눌 수 있습니다.
- 숫자가 5로 끝난다면 그 숫자는 5로 나눌 수 있습니다.
- 짝수는 모두 2로 나눌 수 있습니다.
- 1과 자기자신은 반드시 약수에 포함됩니다.
- 마지막 결과로 나온 80미만의 홀수가 구구단에 속하지 않는다면 그것이 최소 단위 약수 입니다.
- 모든 약수들은 서로 대칭이 됩니다.
모든 약수들은 서로 대칭이 됩니다에 대해서 그림으로 알아봅시다.

그림에 있는 숫자는 48의 약수들입니다.
이 약수들을 크기별로 정리한 뒤 대칭되는 숫자들과 곱해보면 48이 나오는 것을 볼 수 있습니다.
그래서 만약에 이 절반이 되는 기준점의 숫자가 무엇인지 알아낸다면
그 이하의 숫자들중에서만 약수를 구하면됩니다.
대칭이 돼는 숫자들이 알아서 따라 올 것이기 때문입니다.
이제 3588 의 약수를 구해봅시다.
일단 이 숫자를 최대한 나눠봅시다.
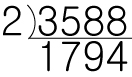
모든 짝수들은 짝수가 나오지 않을때 까지 2로 나누어줍니다.
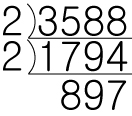
남은 값이 홀수이며 1의자리가 5가 아니라면
3 이나 7 으로 나누어 지는지 확인해 봅니다.
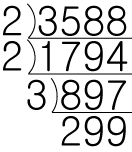
이제 마지막으로 남은 숫자가 정말로 더이상 나누어 떨어지지 않는지 확인하는 작업을 하겠습니다.
#1
10 x 10 = 100 이고
20 x 20 = 400 이니까
299 의 중간에 해당하는 숫자는 10보다크고 20보다 작다는 것을 알 수 있습니다.
그러면 대강 20을 중간 지점이라고 생각합시다.
#2
그리고 299는 홀수입니다. 즉 홀수는 짝수로는 나누어 떨어지지 않습니다.
그렇다는 것은 어쩌면 있을지 모르는 남은 약수의 후보들 중에서 짝수들은 제외할 수 있다는 것입니다.
#3
그리고 이 약수는 무조건 11 이상일 것입니다.
▷4 하고 8은 2x2, 2x2x2 / 6하고 9는 2x3 , 3x3 / 10은 5 x 2 니까
▷4,8,6,9,10 이 숫자들은 아까 최대한 2 , 2 , 3, 이런식으로 나누면서 같이 분해 되었으므로 나올 수 없습니다.
#4
만약에 숫자가 5로 끝난다면 이건 5로 나누어 떨어졌을 것이므로 끝이 5인 숫자도 후보에서 제외할 수 있습니다.
그런 숫자는 11 , 13 , 17 , 19 밖에 없습니다. 즉 만약에 약수가 있다면 이 4가지중 하나일 것입니다.
그러면 이제 299를 11로 , 13으로 , 17로, 19로 나누어서 이중에 약수가 있는지 확인해봅시다.

우연히도 13 으로 정확히 나누어 떨어졌습니다.
23은 구구단에 없는 숫자이므로
이렇게해서 모든 약수의 가장 작은 요소들을 찾았다 라고 할 수 있습니다.
여기에서 잠깐.
Q1. 만약에 #1에서 확인한 중간지점이 1000이면 어떻게 할까요?
이럴땐 11 부터 1000까지 조건에 맞는 숫자들로 일일히 확인 하면서 나눠 봐야 합니다.
그래서 보통 약수는 사람이 구하기보단 컴퓨터에게 시켜서 구하는게 맞습니다.
Q2. 모든 숫자들로 전부 대조해봤는데, 나누어 떨어지는 숫자가 없을 땐 어떻게 하나요?
나누어 떨어지지 않는 그 숫자가 바로 가장 작은 약수중에 하나라 뜻입니다. 즉, 그 숫자 자체가 정답입니다.
만약에 40대 까지 나눠봤는데 더 안나온다면, 더이상 없는 것이라고 생각하고 그냥 넘기는 것이 맞습니다.
수학을 문제로써 낸다면 그 이유는 사람이 풀기 위해서니까요. 우리는 컴퓨터가 아닙니다.
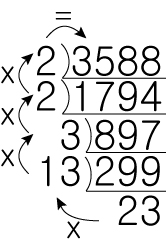
우리는 나누기 작업을 하면서 3588 ÷ 2 ÷ 2 ÷ 3 ÷ 13 = 23 이라는 과정을 거쳤습니다.
그리고 이것을 꺼꾸로 말하자면 23 x 13 x 3 x 2 x 2 = 3588 이라는 뜻도 됩니다.
이걸 다르게 줄여서 말하자면 23 x 13 x 6 x 2 = 3588 이라는 말도 될것이고
23 x 13 x 3 x 4 = 3588 이라는 말도 될 것입니다.
이렇게 만들어 지는 모든 숫자들도 약수중의 하나입니다. 이제 이런 모든 약수들을 추려보는 시간입니다.
2,2,3,13,23 이라는 5개의 숫자를 사용해서 만들수 있는 모든 숫자들을 구하는 것 입니다.
2x2 = 4
2x2x3 = 12
2x2x3x13 = 156
2x2x3x23 =276
2x2x13 = 52
2x2x23 = 92
2x3 = 6
2x3x13 = 78
2x3x13x23 = 1794
2x3x23 = 138
2x13 = 26
2x13x23 = 598
2x23 = 46
3x13 = 39
3x13x23 = 897
3x23 = 69
13x23 = 299
그리고 2 , 3 , 13 , 23과 1, 3588를 포함해서
3588의 약수는1,2,3,4,6,12,26,39,52,69,78,92,156,276,299,598,897,1794,3588 가 됩니다.
예시로 들은 문제는 나누기를 할때 나머지가 101이상의 홀수일때의 문제점을 설명하기 위해서 큰숫자를 사용했기 때문에 약수로 매우 많은 수가 나왔습니다만,
만약에 관련된 문제들을 풀게 된다면 보통 2x3x13 같이 적은 숫자들을 조합해서 풀기 때문에 실제로 이렇게 여러개의 약수를 구할일은 없습니다. 사용하기 위해서 구한다고 해도 컴퓨터로 처리합니다.
다만 이러한 과정을 통해서 약수들을 구한다는 것을 제대로 이해하고 넘어가시면 됩니다.
최대공약수(3/3)
이제 약수 사용하는 예시봅시다.
8 ÷ 4 , 12 ÷ 6 , 14 ÷ 7 모두 정답은 2입니다.
그리고
4 ÷ 8 , 6 ÷ 12 , 7 ÷ 14 는 분수로 4/8 , 6/12 , 7/14 로 표현됩니다.
그리고 이것들의 크기가 1/2 과 같다는 것을 분수를 배우면서 설명했었습니다.
그렇다면.
8 ÷ 4 , 12 ÷ 6 , 14 ÷ 7 이렇게 적어서 사용할 것이아니라
좀더 보기 편하게 2 ÷ 1 이라고 적어서 쓸수 있지 않을까요?
이렇게 큰 숫자를 작은 숫자로 바꿔서 사용할 때 사용하는 것이 바로 최대공약수입니다.
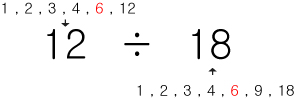
12와 18이 가지고있는 약수들을 봤을때
둘다 가지고 있는 약수중에서 가장 큰 숫자를 최대공약수 라고 합니다.
최대 공약수의 특징은, 계산할때 쓰이는 숫자들의 크기를 줄일 수 있다는것입니다.
즉 12 ÷ 18 의 양쪽 숫자에 6을 나누면2 ÷ 3 이 됩니다.
8 ÷ 4 가 결국 2 ÷ 1 하고 같은 결과인것 처럼,
12 ÷ 18 은 2 ÷ 3 하고 결과가 같다 라고 생각할 수 있겠습니다.
최대공약수를 구하기 위해선 모든 약수를 구할 필요가 없습니다.
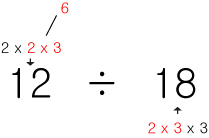
12와 18은 위의 계산으로 나눠보면 2 x 2 x 3 과 2 x 3 x 3 이 나올 겁니다.
이중에서 둘다 가지고 있는 것들을 비교해서 모두 모은 뒤에 곱하면 그게 최대공약수 입니다.

이렇게 둘을 같이 묶어서 약수 구하기를 진행하고,
그 중에 옆면에 나오는 숫자들을 모두 곱해서 구하는 방법도 있습니다.
만약 최대공약수를 구하는 것이 목적이 아니라 숫자를 줄이는 것이 목적이라면,
아래에 나온 결과 나머지들을 2 ÷ 3 으로 그대로 쓰셔도 됩니다.
2.배수의 개념(1/2)
배수란 '몇 배' 인지 가늠하기에서 썻던 그 배 를 뜻합니다.
9는 3의 3배일 것이고 , 12 는 3의 4배일 것입니다.
그 3의 1배,2배,3배..... 에 해당하는 6,9,12의 모든 숫자들을 3의 배수 라고 합니다.
여기에서 말하는 배수의 범위는 9배를 넘어서 10배가 될수도 100배가 될수도 있습니다.
즉 배수의 범위는 끝이 없습니다.
최소공배수

배수 중에서 둘다 가지고 있는것, 그중에 가장 작은것을 최소공배수 라고 합니다.
최소공배수는 두 숫자를 똑같은 숫자로 만들어서 제대로 비교하고 싶은데
그 똑같은 숫자가 몇이 되어야 하는지 알고자 할때 사용합니다.
다음 글에서 이와 관련된 사용법을 알아볼 것입니다.
만약에 두 숫자가 최대공약수가 없는 숫자라면
그대로 둘을 곱해서 최소공배수를 구할 수 있습니다.
예를 들자면 4 와 7 의 최소공배수는 4x7 인 28 입니다.
만약에 두 숫자가 최대공약수가 있는 숫자라면
최소공배수는 이렇게 구할 수 있습니다.

서로의 나머지값을 곱해주면 나옵니다.
즉 27 x 5 = 135 고 45 x 3 = 135 입니다.
그러므로 27 과 45의 최소 공배수는 135 라고 할 수 있습니다.
'수학 > 초5' 카테고리의 다른 글
약분과 분수의 곱셈 (1) 2022.02.11 분수의 종류(short) (0) 2022.02.11 숫자의 범위와 어림하기 (0) 2022.02.09 덧셈 / 곱셈 예측 능력 키우기 (short) (0) 2022.02.08 괄호를 이용한 계산 순서 바꾸기 (short) (0) 2022.02.08