100을 넘는 숫자를 한 숫자로 나누기

https://mytory.tistory.com/26?category=987800 

곱하기와 나누기

 

나누기에 대한 개념은 이곳에서 확인하실 수 있습니다.

이번엔 간단하게 100을 넘는 숫자를 나누는 방법만 알아보겠습니다.

---

 

318 ÷ 3 을 예시로 같이 풀어봅시다.

 

아래의 그림을 보겠습니다.

 

 

먼저 나누기를 하기 위해서 이렇게 선을 그어 줍니다.

선을 긋는 것이 필수는 아닙니다. 개념을 이해하기 위해 그었습니다.

 

 

우리는 318을 숫자 한개씩 한개씩 읽어가면서 풀것입니다.

먼저 318 중의 3 을 봅시다. 3으로 3 을 몇번 뺄 수 있을까요?

3 x 1 = 3 이니까 우리는 3으로 3을 1번 뺄 수 있습니다.

 

 

다음으로 1은 3으로 몇번 뺄 수 있을까요?

1이 3보다 작기 때문에 3을 뺄 수 없습니다.

우리는 0 이 없음 을 뜻한다고 했습니다.

그러니까 이렇게 적어줍시다.

 

 

아까전에 빼지못한 1 은 그대로 같이 내려옵니다.

그래서 빼야할 숫자는 18이 됩니다.

18은 3으로 몇번 뺄 수 있을까요?

3 x 6 = 18 이니까 우리는 3으로 18을 6번 뺄 수 있습니다.

 

 

이것을 통해서 318 ÷ 3 = 106 이라는 답이 나옵니다.

그리고 반대로 106 x 3 을 하면 정답은 318 이 됩니다.

---

하지만 만약에 이런경우는 어떨까요?

119 ÷ 3 을 해봅시다.

 

 

3으로 1은 나눌수 없습니다. 우리는 0은 없음 이라고 했습니다.

0이 중간이나 끝에 쓰이는것이 아니라면 이런경우엔 안쓰고 넘어갑니다.

 

 

그러면 11 을 3으로 몇번 뺄 수 있을까요?

3 x 4 는 12 지만 12는 11보다 큽니다.

그러면 11하고 가까우면서 가장 큰수는

3 x 3 은 9 가 되겠습니다. 그러니까 3번 뺄 수 있겠군요.

 

 

11 에서 9를 빼고 2가 남았습니다.

그리고 이럴때는 2를 포함해서 29 로 생각하는겁니다.

29 보다 작으면서 가장 가까운 숫자가 무엇일까요?

3 x 9 = 27 즉, 29에서 3 을 9번 뺄수 있습니다.

 

 

그러니까 119 ÷ 3 의 정답은 39 입니다. 그리고 나머지가 2 입니다.

이것을 반대로 해서 39 x 3 + 2 = 119 가 됩니다.

 

또한 나누었을때 나머지가 남았으므로, 이것을 분수로

 

 

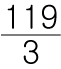
이렇게 표현 할수도 있고 (가분수 라고 합니다.)

 

 

이렇게 표현 할 수도 있습니다. (대분수 라고 합니다.)