분수와 정수의 관계, 그리고 소수

https://mytory.tistory.com/29?category=987786 

분수와 크기 비교

이전 글에선 분수의 개념이 무엇인지 살펴 보았습니다.

 

https://mytory.tistory.com/28?category=987786 

100을 넘는 숫자를 한 숫자로 나누기

그리고 숫자를 나누기 하면서, 우리는 가분수를 정수로 바꾸는 방법을 배웠습니다.

 

이번에는 배운것들을 응용해서 분수와 정수간의 관계를 알아보겠습니다.

---

1.정수에게 분수란?

 

 

우리는 앞서 곱하기는 2 x 3 은 2를 3번 더하는 것이라고 했었습니다.

그런데, 2개를 1/2 번 (2분의 1번) 더하라니 도대체 무슨 말일까요?

 

우리는 앞서 1/2이 1개를 두조각내서 두조각중에 한조각이 남은 것이라고 했습니다.

그러면 이걸 반대로 생각해봅시다.

 

 

반조각을

 

 

2번 하면? 이것은 2/2 입니다. 그리고 2/2 는 1하고 같다고 했었지요.

즉, 2 x 1/2 는 1입니다.

그리고 2 ÷ 2 는 1입니다.

 

우연일까요? 다시해봅시다.

 

 

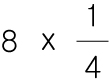
1/4개를 8번 더해봅시다.

 

4/4 가 2개가 나왔습니다.

4/4도 1이니까 1x2 는 2라는 결과가 나옵니다.

즉, 8 x 1/4 = 2 입니다.

그리고 8 ÷ 4 는 2입니다.

 

그렇다면 이것을 이렇게 써보는 것은 어떨까요?

8 x 1 ÷ 4 = 2 를 순서대로 풀어봅시다.

8 x 1 = 8 ,

8 ÷ 4 = 2

이것이 / 와 ÷ 가 같은 뜻인 이유입니다.

즉, 정수에게 4 라는 '분모'는 나누기 라는 뜻입니다.

8 ÷ 4 = 8 x 1/4 이라는 뜻입니다.

 

그렇다면 이런 경우는 어떨까요?

 

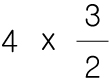
차근차근히 생각해봅시다. 일단 3/2 라는 가분수를 바꿔서 표현하자면,

 

 

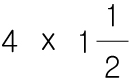
이렇게 됩니다. 그리고 이것은 1개하고 반을 뜻하니까 이것을 4번 반복하면

 

 

 

총 6개가 나옵니다.그러니까 4 x 3/2 = 6 개 라는 것을 알 수 있습니다.

 

그런데 우리는 아까 분모가 나누기 하라는 뜻 하고 같다는 것을 알았습니다.

그렇다면, 아까 전에 알아낸 사실대로 계산해본다면 어떨까요?

4 x 3 ÷ 2 =?

4 x 3 = 12

12 / 2 = 6로 같은 답이 나오는 것을 알 수 있습니다.

 

그러므로, 정수에게 분모란(↓) 나누기 라는 뜻이고, 정수에게 분자란(↑) 곱하기 라는 뜻입니다.

 

 

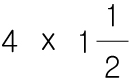
분수에 붙어있는 정수는 말그대로 원래 곱하기에 사용햇던 것과 같습니다.

하므로 정수를 굳이 가분수로 바꿔서 계산할 필요 없이

 

4 x 1(분수에 붙어있던 정수) = 4

4 x 1/2 = 2

로 따로 구한 뒤에 2 + 4 를 해주면 됩니다.

---

2.정수가 붙은 분수 와 가분수를 서로 바꾸기

 

일단 미리 말씀드립니다. 보기좋게 바꾼 분수를 굳이 다시 가분수로 바꾸는 것은 실제로 전혀 필요 없습니다.

'일부를 정수로 정리하는것'이 분수 계산의 마지막 단계란 것을 생각하면 쉽습니다.

즉, 선물포장 다해놨는데 뒤늦게 아 이거 빠트렸어요 할때 다시 풀어 해치기 위해서 쓰입니다. 

 

 

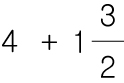
4부터 가분수로 만들어 봅시다.

4 x 1 은 4 입니다.

그리고 2/2도 3/3도 모두 1이라고 했습니다.

그렇다면 이것을 이렇게 바꿀 수 있을 것입니다.

 

 

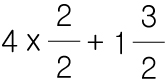
4 x 2 / 2 를 아까전 대로 풀어 봅시다.

4 x 2 = 8 입니다.

그러면 8 / 2 가 남습니다.

이걸 그대로 써주면 가분수가 완성됩니다.

 

 

 

이제 오른쪽(→)의 숫자도 가분수로 만들어 줍시다.

(정확히는 누군가가 계산을 하다가 말은 가분수를 가분수로 만들어 봅시다.)

 

1 과 3/2 은 1개와 3/2조각이 있는 것으로 볼 수 있습니다.

그런데 여기에서 1하고 2/2 는 같은 것이라고 했습니다.

즉 ,

 

 

 

1과 3/2은 2/2 + 3/2 하고 같다고 할수 있습니다.

 

 

이렇게 구한 가분수들을 더하면 가분수로 구하는 정답은 13/2 가 됩니다.

(쓸일은 없으니 버리세요)

 

이제 제대로 가분수를 정수로 바꿔서 푸는 방법을 알아봅시다.

 

 

다시 처음으로 돌아 왔습니다. 먼저 가분수를 정수로 만들어 줍시다.

 

3은 2로 몇번 뺄수 있을까요? 2 x 1 은 1 입니다. 즉 1번 뺄수 있습니다.

 

 

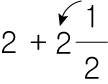
빼고 나서 나머지를 분자에 적어줍니다.

1번 뺄수 있었으므로 원래있던 정수에는 + 1 을 해줍니다.

 

 

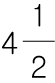
이제 정수끼리 더해주면 그것이 정답입니다.

---

3.소수

 

모든 글씨는 오른쪽(→) 으로 쓰며 오른쪽으로 읽습니다.

지금 보고있는 한글 또한 그렇지요.

 

하지만 분수를 사용하기 위해선 글씨를 위와 아래로 정렬해왔습니다.

현재도 1/2 식으로 사용은 하고 있으나,

1과 1/2 같이 정수가 붙어 있을 때는 한글을 섞어서 써야만 합니다. 이런경우, 외국인들은 못알아 볼 것입니다.

 

그래서, 분수를 표현할때 글씨를 오른쪽으로 써가면서 편하게 표현하기 위해서 소수 라는 것이 생겼습니다.

소수에 대한 자세한 설명은 초3 과정을 넘어가기 때문에, 개념만 익힌뒤 다음에 보겠습니다.

 

1/2 은 1보다 작습니다. 하지만 1/2 은 0보다 큽니다.

그래서 우리는 1보다 작은 수를 분수없이 편하게 표현하기 위해서 다음과 같이 쓰게 되었습니다.

 

 

소숫점 : 1의 자리보다 작다는 것을 알리는 소수의 시작 점 입니다.

소수 : 0보다 크고 1보다 작은숫자를 표현한 것입니다.

 

여기에서 0.1 은 1/10 크기를 뜻합니다.

0.2 는 2/10 을 뜻하고

1.5 는 1과 5/10를 뜻합니다.

 

그리고 5/10 는 1/2 을 5번 나눈 것과 같으므로

5/10 은 1/2 과 크기가 같습니다.

즉,

 

 

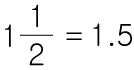
1과 1/2 은 1.5 와 크기가 같으므로, 1.5라고 편하게 적을 수 있습니다.