곱하기와 나누기

https://mytory.tistory.com/17?category=987783 

수학의 기초

 

이 글은 위의 글에 있는 구구단에 대한 설명이 포함 되어있습니다.

구구단을 외우지 않았더라도 이 글을 이해하실 수 있으나

꼭 전부 외우지 않으면 수학을 할 수가 없습니다.

 

---

1.곱하기 / 곱셈 / 곱

 

단어를 읽고 사용하는 방법은 덧셈/뺄셈과 같습니다.

3 x 3 = 9 를 삼 곱하기 삼 은 구 라고 읽으며

곱하는 행위 자체를 곱셈이라고 하기도 합니다.

또한 3 x 3 = 9 를 삼 과 삼의 곱은 구 라고 읽을 수도 있습니다.

 

먼저 곱하기의 개념을 그림을 보며 이해해봅시다.

 

 

여기에 붉은 원 2개가 있습니다.

 

 

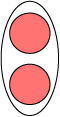
이 두개의 원을 비닐 봉지에 담았다고 생각해 봅시다.

 

 

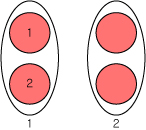
그리고 이 비닐 봉지가 2개가 있다면

이 때 붉은 원의 갯수는 몇개 일까요?

붉은 원이 2개 그리고 비닐봉지가 2개니까

2 x 2 입니다.

그러면 정답은 4개 입니다.

 

그렇다면

 

 

비닐 봉지가 3개가 된 다면 붉은 원은 몇개 일까요?

똑같이 해본다면 이건 2 x 3 이니까

정답은 6개 입니다.

 

 

마지막으로 확인해봅시다.

 

그리고 붉은 원이 3개씩 , 비닐봉지가 3개 면

3 x 3 = 9개가 됩니다.

 

이러한 개념을 곱셈이라고 합니다.

 

구구단은

붉은 원이 몇개 들어있고

그 비닐봉지는 몇개 일때

총 붉은 원의 갯수가 몇개인지 2 x 1 부터 9 x 9 까지의 정답을 적어놓은 것입니다.

 

그리고 이 정답들을 구구단이라는 이름으로 외워두는 이유는,

일일히 생각하면서 쓰기엔, 너무 많이 너무 자주 사용하기 때문에

그 때마다 계산해서 쓸수 없기 때문입니다.

---

2.나누기 / 나눗셈 / 나눔

 

나누기 또한 마찬가지로 그림을 보며 파악해봅시다.

 

 

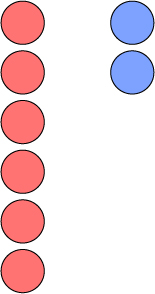
붉은 원이 6개 푸른 원이 2개 있습니다.

 

 

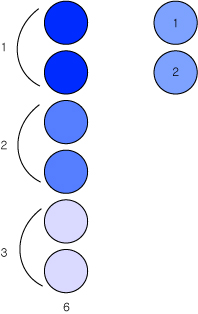
푸른 원의 갯수가 2개니까 6개는 2개로 3번 나눌 수 있는 것을 볼 수 있습니다.

이를 다른 말로 표현하자면, 6을 2로 몇번 뺄 수 있는가 라고 생각해 볼 수도 있습니다.

이것을 우리는 6 ÷ 2 = 3 (육 나누기 이 는 삼) 이라고 읽습니다.

나눗셈은 꼭 오른쪽→ 으로 읽어가면서 처리해야 합니다.

 

나눗셈을 하면서 이런 경우도 발생할 수 있습니다.

 

 

이렇게 나눗셈 뒤에 남은 빨간 원 하나를 나머지 라고 합니다.

이런 경우엔 7 ÷ 2 = 3 ... 1 (7 나누기 2 는 3 나머지 1) 이라고 적습니다.

 

번외로 수학 말고 컴퓨터 상에서는 나머지를 7 % 2 = 1 이라고 씁니다.

 

이 부분은 분수를 다룰 때 다시 보겠습니다.

---

3.덧셈 뺄셈 곱셈 나눗셈의 순서

 

'나눗셈과 곱셈' 또한 '덧셈과 뺄셈' 처럼 오른쪽(→) 으로 읽어가면서 계산합니다.

 

또한 덧셈의 반대는 뺄셈 , 곱셈의 반대는 나눗셈 이라고 생각해도 됩니다.

 

 

8 x 3 ÷ 3 = 8

9 ÷ 3 x 3 = 93 + 1 - 1 = 35 - 2 + 2 = 5 입니다.

 

하지만 그렇다고 해서 오른쪽(→) 으로 읽어가면서 풀어야 된다는 것을 간과해서는 안됩니다.

 

9 ÷ 3 x 3 = 9 를 예로 들자면 이런것입니다.

 

9 ÷ 3 = 3 입니다.그리고 3 x 3 = 9입니다.이것이 올바른 풀이 법입니다.

 

그런데 이걸 순서를 무시하고 왼쪽(←) 으로 읽으면서 풀면3 x 3 을 먼저 풀어서 9가 되고9 ÷ 9 = 1이됩니다. 다른 답이 나온 것을 볼 수 있습니다.이것은 틀린 풀이 법 입니다. 때문에 꼭 오른쪽(→)으로 읽어가며 풀이해야 하는 겁니다.

 

이것은 더하기 와 곱셈 , 빼기 와 나눗셈 등등을 섞었을때도 생겨나는 문제 입니다.

9 x 2 + 1 = 19 지만

이걸 꺼꾸로 읽으면 답이 20 이 되어 버립니다.

 

이런 문제로 곱셈과 나눗셈은 특수한 규칙이 하나 세워져 있습니다.

1 + 9 x 2 = ? 이라는 문제를 푼다면

곱하기를 먼저 풀은 다음에 덧셈을 해야 하는 규칙 입니다.

즉 위의 답은

9 x 2 = 18 , 18 + 1 = 19

순으로 풀어서 정답은 19 입니다.

마찬가지로 10 - 3 ÷ 3 = ? 를 풀 때도

3 ÷ 3 = 1 , 10 - 1 = 9 순으로 풉니다.

 

10 - 2 x 6 ÷ 3 + 4 = ? 는

2 x 6 = 12, 12 ÷ 3 = 4, 10 - 4 = 6, 6 + 4 = 10 순으로 풉니다.

 

즉, 곱셈과 나눗셈을 먼저풀고, 나온 답으로 덧셈과 뺄셈을 하면 됩니다.

 

 

---

3.분수

 

이런 경우엔 어떻게 할까요?

2 ÷ 3 = ?

3 ÷ 2 = ?

이렇게 나눠야 돼는 숫자가 기준보다 작거나,

나눴을때 나머지가 생길 때는 이것을 어떻게 표현 할까요?

그래서 이런 경우를 제대로 표현하기 위해서 존재하는 것이 분수 입니다.

즉, 이렇게 쓸 수 있습니다.

 

 

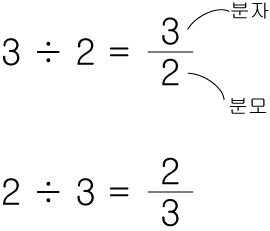
이때, 위쪽으로 올라가는 첫번째 숫자를 분자, 아래쪽 숫자를 분모 라고 합니다.

그중에서 분자가 분모보다 크다면 그것을 가분수 라고 합니다.

 

컴퓨터 상에서는 3/2 , 2/3 으로 작성해서 쓰입니다.

---

https://mytory.tistory.com/28?category=987786 

100을 넘는 숫자를 한 숫자로 나누기

 

나누기를 분수로 만드는 자세한 과정은 초3 과정에서 확인하실 수 있습니다.