-
연립방정식과 부정방정식수학/고1 2022. 6. 3. 20:33
연립방정식의 개념은 이전에 중학교 과정에서 다룬적이 있습니다.
이번 과목은 기초적인 개념외에 고등과정에서 추가로 배우게 되는 항목들을 정리했습니다.
y=ax 형태의 함수 식의 연립은 이전 글을 참고해주세요.
+2022-11-22 링크 수정 및 잘못 정리된 수식 대량 수정 , 문맥 정리
1.연립방정식
1)해가 없음

연립방정식의 결과로
0A=0 가 나올경우 두 식은 항등식이라는 뜻입니다.
0A=n 의 형태로 나올경우 두 방정식 간에는 해가 존재하지 않는다는 뜻입니다.
2)삼항 연립방정식

서로 분리되어있는 미지수 3개가 합연산으로 구성되어있는 식에서 사용되는 연립방정식입니다.
부분적으로 2개씩 연산하여 미지수 1개를 제거한뒤, 제거한 두 식을 연립합니다.
3)이차 연립방정식

어떤 변태가낸 문제인지 궁금하군요두 이차식의 연립방정식은 서로의 식을 뺀 뒤에 2차식이 남지 않도록 인수분해를 해줍니다.
식의 결과값이 0 이 아니라 예시처럼 4일 경우엔
인수의 갯수만큼의 숫자 n개의 곱으로 결과 4를 만드는 모든 경우를 추려냅니다.
이에 따른 결과를 각각의식 A와 B에 대입하고 , 모두 만족하는 해를 찾습니다.
이렇게 추리는 계산을 하기 위해선 결과가 정수의 곱으로 이루어져 있을때를 알때만 한정됨을 기억합시다.
3x4/3 , 5x4/5 등의 셀수없이 많은 수가 존재합니다!
보통은 두 식의 결과가 영등식으로 나타나는 문제를 풀게 되기 때문에
이렇게 모든 경우를 추리할 필요가 없습니다.
영등식의 예를들어 만약 두 식의 연립 결과가 (x+y)(2x+y)=0 으로 정리 되었다면
x=y 혹은 2x=y 이므로
이를 식 A와 식 B에 둘다 대입하여 x 하나에 대한식이나 y 하나에 대한 식으로 바꾼뒤
함수식의 연립으로 해결합니다.
※ 함수식의 연립 방법은 상단 링크를 참고해주세요.
4)삼차 연립방정식
⑴
만약 고차방정식이라면 위와 동일한 방법으로 계산할 수 있습니다.
⑵

만약 두 식이 삼차방정식이며 일차 x항과 일차 y항이 없다면
이차방정식만 남도록 조정한뒤 인수분해를 진행합니다.
즉 , 가장 높은 최고차항은 식을 변형해서 연립 결과에서 제외할 수 있습니다.
⑶

두 식을 연립해서 2차식만 남을 경우
x에 대한 내림차순으로 정리한뒤 근의 공식으로 근을 구해서 진행할 수도 있습니다.
2.부정방정식
1)개념

해를 구하기위한 식의 갯수가 모자른 방정식을 부정방정식이라고 합니다.
미지수를 2개 이상 지니고있는 단일식도 이에 해당합니다.
부정 방정식은 식을 만족하는 모든 해를 구할 수는 없습니다.
①을 예시로 들면 x=1 y=-1 , x=2 y=-2 , x=3 y=-3 등의 셀수없는 해의 쌍들이 존재할 것입니다.
그래서 두가지 예외적인 규칙이 있습니다.
⑴정리가 완료된 각 항의 값의 결과는 0으로 취급
⑵정리한 식의 결과가 영등식일 때만 취급
⑶식을 곱에 대하여 완전히 인수분해 했다면 기존의 방식을 따를 것
아래의 예제들을 보며 이해해봅시다.
2)x,y의 이차 부정방정식
⑴
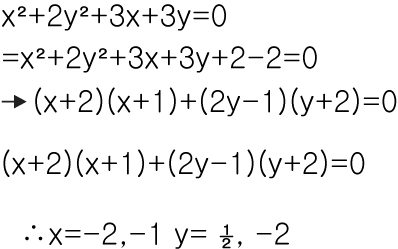
만약 항의 결과가 0이라고 정의하지 않을 경우
y값은 ½보다 작은 숫자에서 음수가 되며 해의 갯수는 무한히 많아 집니다.
만약 이 부정 방정식의 해가 =0의 영등식이 아닐경우
각 항을 0 으로 취급할 수 없음에 따라 그 결과는 무한히 많아질 것입니다.
위의 식에 대한 정리는 xy 가 둘다 곱되어있는 항이 없는
x와 y의 이차방정식을 x인수+y인수 형태로 변형합니다.
⑵

x일차항 또는 y일차항이 존재하지 않을때 xy인수 + y인수로 정리합니다.
⑶

식을 곱에 대하여 완전히 인수분해 했다면 기존의 방식을 따를 것 이므로
이번의 경우엔 결과를 만들 수 있는 모든 경우를 추려냅니다.
곱으로 1을 만드는 경우의수는 (1x1 | -1x-1) 가 존재합니다 그러므로 해는
x=2±1 , y=-4±1 가 됩니다. (복부호동순)
3.근과 계수의 연립방정식
1)

m+n=b , mn=c 의 연립 방정식은 x²-bx+c의 근과 같습니다.
2)

(x+y=3,xy=4) 와 (x+y=-3,xy=4)의 단위로써 해는 두쌍이 됩니다.
3.응용
A1)

인수분해 식으로 정리할 수 없을때의 부정방정식의 근은
판별식 D를 사용해서 근이 성립하는 범위를 구합니다.
