[적분] 정적분

 

정적분의 범위는 컴퓨터 작성상의 한계가 있습니다.

작자는 정적분의 범위를 ∫²₁ 로 작성하고 있으며 이는 2-1의 범위를 의미합니다.

첨자에 미지수나 수식입력이 불가능한 경우 (a~b)∫{ ƒ(x) }Δx 로 작성합니다.

시그마는 ∑(k : 1~n), 극한은 lim(n→∞) 혹은 (n→∞) 로 작성합니다.

---

1.개념

 

[정적분]

 

1.정의

 

 

본래의 적분 계산방법을 의미합니다.

∫ : 합을 뜻하는 S의 모양을 따온 기호입니다

ⁿₓ : dx축 상에서 a는 아래끝 b는 위끝이며 [a,b]의 범위를 의미합니다.

 

---

2.정석적인 계산법

 

 

 

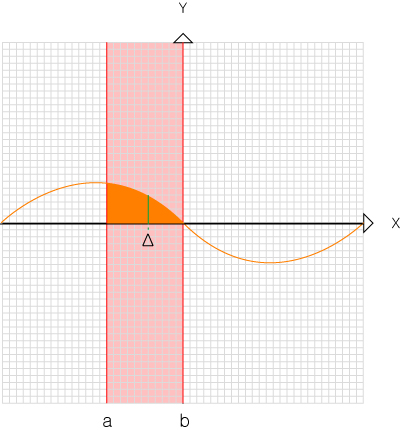
선의 가로길이를 Δ라고할때 a~b사이의 모든 선의 넓이를 더한다는 의미입니다.

 

위의 식을

(a~b)∫{ ƒ(x) }Δx = (n→∞) ∑(k : 1~n) ƒ(a+(b-a)k/n)((b-a)/n)

라고하겠습니다. 순서대로 해독해봅시다.

 

1.(a~b)∫ : 그래프상 x=a 에서 x=b 지점까지

2.ƒ(x)Δx : ƒ(x)를 x로 적분한다.

3.lim(n→∞) : a~b 까지의 거리를 무한히 쪼개서 미세하게 만들고

4.∑(k:1~n) : 그 미세한 모든 거리들을 다음 수식에 기준하여 더한다.

5.ƒ(a+(b-a)k}/n) :

→

a+: 시작점a에서부터 ,

(b-a) :  b까지,

k/n : 의 전체 선의 갯수인 n개 중의 k번째의 값,

ƒ() : 에대한 y값(높이)

6.(b-a)/n : a~b까지의 모든거리를 n개로 나눴을때의 x지점 하나의 (너비)

 

---

3.차이에 의한 계산법

 

 

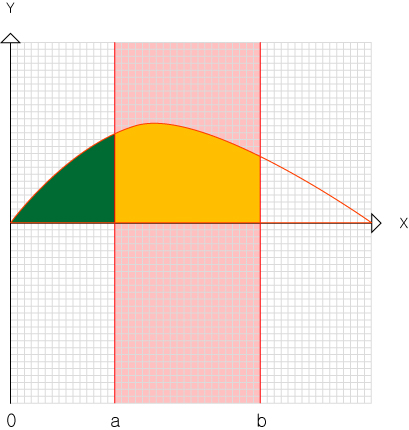
초록 범위와 노란범위의 합을 연두색 이라고 하면

연두색 - 초록색 = 노란색이 됩니다.

정적분은 이를 활용해서 구합니다.

 

정적분을 이와같이 정의할때.

ƒ(x)=2x 를  ∫²₁ 의 범위에 대해서 정적분을 한다면 F(2)-F(1)이므로

{2²+C}-{1²+C} = 3

여기에서 두 부정적분의 차를 통해서 상수C는 제거됩니다.

 

 

정적분 결과를 원시함수로 작성할때 원시함수는 위와 같이 나타냅니다.

 

---

4.정적분의 미분

a~x 범위의 정적분을 하나의 점에 대해서 표현한다면,

즉 lim(x→a) 일때

F(x)-F(a) 라고 표현한다면

미분식 1 / (x-a)를 곱했을때

 

 

F(a)에 대한 미분이 성립하여 결과는 ƒ(a)가 됩니다.

그러므로 ƒ'(a)↔ƒ(a)↔F(a) 가 성립합니다.

 

다만 , 이때 x는 끝값으로써 대입 되어지는 숫자이기 때문에

이때 본래의 원시함수는 (a~x)[F(t)]의 t에 대한 식이 기준이 됩니다.

 

주의할 점이 한가지 있습니다.

적분을 먼저한 뒤에 미분을 하면 상수항이 생긴뒤에 사라지므로 큰 문제가 안되나,

미분을 먼저한 뒤에 적분을 하면 상수항이 사라진뒤에 미지의 상수항 C가 생성되어 버립니다.

 

---

2.응용

 

[확장 지식]

 

가우스의 분리합

 

∫(0~2)[x-1]

가우스는 x의 값이 1보다 작고 클때 그래프가 갈리므로

∫(0~1) + ∫(1~2) 로 나눠서 계산할 필요가 있습니다.

 

∫(0~1)[x-1] = -1 (x=1 의 범위에서 모든 구간의 높이가 -1 이므로 1×-1=-1 )

+∫(1~2)[x-1] = 0

∴ -1  

 

---

절대값의 분리합

 

 

∫(0~2)|x²-1| 는 (x≥1, x<1) 에 대해서 

∫(0~1)(-x²+1)+∫(1~2)(x²-1) 의 식이 됩니다.

 

---

조건함수의 분리합

 

 

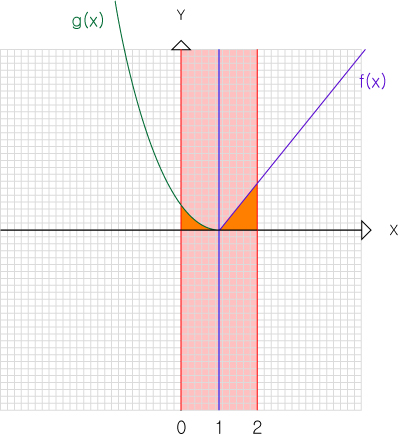
∫(0~2)h(x)= {x≥1 : ƒ(x) , x<1 : g(x)} 

→∫(0~2)=∫(0~1)+∫(1~2) 

이때 ∫(0~1)g(x)+∫(1~2)ƒ(x) 의 식이 됩니다.

 

---

[필수]

 

적분의 도함수

ƒ(x)=(0~x)∫{ 2t+1 }Δt 

만약 미분식 d/dx 를 곱하면

식에서 적분을 미분하여 원래의 함수만 남게 되므로

∴ ƒ'(x)=2x+1

 

d/dx 를 곱한다는 의미는 극미한값 Δ / Δx 를 곱해서

식을 Δƒ(x)/Δx 로 만든다는 뜻입니다.

그러므로 범위 (0~x)는 미분식의 성립에는 영향을 주지 않습니다.

 

상수~x로 쓸 경우 F(x)-상수 의 형태가 되므로

미분법에 의해 상수가 사라짐에 따라 반드시 성립합니다.

이때 F(t) 를 F(x)로 주체를 바꾸는 의미가 존재합니다.

 

---

[풀이]

 

 

= F'(1)+2'F(1)

 

---

[테크닉]

 

①

 

 

②

극한값 대입에 의해 b+a는 2a가 됩니다.