[적분] 부정적분

 

여기에서 말하는 부정적분은 '부정 적분' 이 아니라 '부 정적분' 입니다.

작자는 가독성을 높이기 위해서 적분을 ∫{ ƒ(x) }Δx 의 형태로 작성하고 있습니다.

실제로는 중괄호를 작성하지 않아도 됩니다.

---

 

1.개념

 

[적분]

 

1.정의

 

 

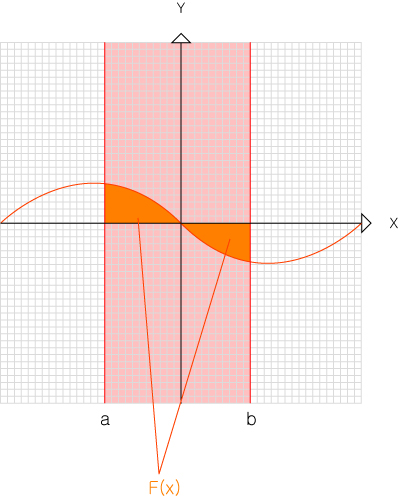
임의의 범위 a~b에 대해서

축과 그래프 / 그래프와 그래프 사이의 면적을 의미합니다.

다른 그래프 없이 한개의 그래프에 대한 적분은 x축과의 면적을 의미하게 됩니다.

 

 

이때 ƒ(x)에서 계산과정을 거쳐서 완성된 함수 F(x)는 원시함수라고하며

위의 식에서 ƒ(x)는 적분 대상, 적분함수,

dx는 적분변수 를 의미합니다.

dx 는 미분에서 사용되었던 Δx 로써 x를 기준으로 적분했다는 의미가 있습니다.

 

미분과는 역함수의 관계를 지니고 있습니다.

즉, ƒ'(x)↔ƒ(x)↔F(x) 사이의 변형이 이루어질 수 있으며

식으로는 (d/dx)·∫{ ƒ(x) }Δx = ƒ(x)를 만족합니다.

 

범위 [a,b] 에 대한 부분과 Δx가 나오는 이유는 다음 과목인 정적분 에서 소개합니다.

 

---

2.그래프 특성

 

①

 

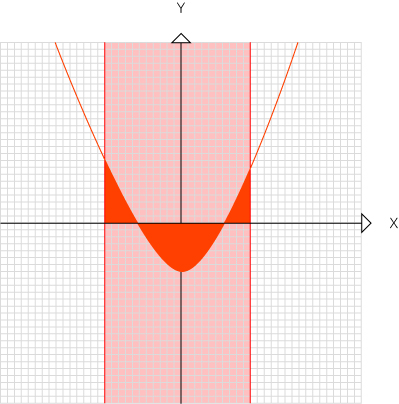
적분은 x축(비교대상) 보다 낮은 위치에서 음의면적을 지닐 수 있습니다.

그러므로 특정 범위의 적분값은 합산 되면서 0이 되거나 작은 값이 나올 수 있습니다.

만약 구하고 싶은것이 '넓이' 라면 절대값인 |f(x)|에 대한 적분을 구할 필요가 있습니다.

 

②

 

x축에 대한 주기함수일 경우 한 주기마다 적분의 합의 값은 0이 됩니다.

그러므로 F(x)=F(x+p) 가 성립합니다.

 

③

 

 

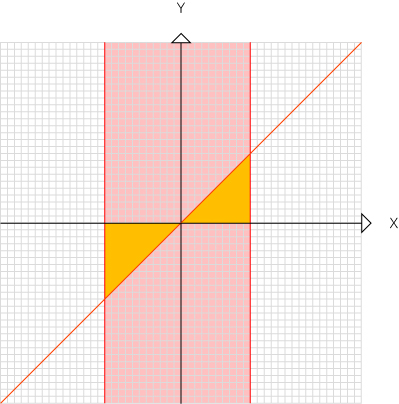
일차함수는 삼각형의 넓이를 구함으로써 적분을 대체할 수 있습니다.

 

---

3.부정적분

 

적분이 미분의 역함수라는 점을 이용하여 미분법을 반대로 합니다.

그러므로 부정적분을 하기 위해선 인수분해 식을 풀어낸뒤 적용해야 합니다.

계산의 특징상 상수항C를 구할 수 없기 때문에 부 정적분이라고 불립니다.

 

ƒ(x) = 3x²+2x+1 에서 3x³+2x²+x+C 로 올린뒤 올린 지수만큼 계수를 나눠서

F(x)=x³+x²+x+C가 됩니다.

 

---

2.응용

 

 

[확장 지식]

 

적분과 최대차항

F(x)+ƒ'(x)=x³+bx 일때 

F(x)는 3차함수 f(x)는 2차함수 f'(x)는 1차함수

 

 

조건함수의 적분

f(x)={x≤-1 : x , x>-1 : k} 일때 

F(x)={x≤-1 : ½x² , x>-1 : ½k²}

 

---

[기본]

 

①

∫{ (x+1)² }Δx

= ∫{ x²+2x+1 }Δx

= ⅓x³+x²+x+C

 

②

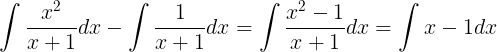
적분식은 같은 범위와 같은 대상 dx에 대해서 서로 묶어 쓸수 있습니다.

 

③

등식의 양변을 적분합니다.

 

④

∫{ ƒ'(x)+2x }Δx

= ƒ(x) + x²+C

 

⑤

∫{ xƒ'(x) }Δx = x²

→xƒ'(x)=2x(양변을 미분)

→ƒ'(x)=2

∴ f(x)=2x+C(양변을 적분)

 

 

[풀이]

 

 

적분식의 최고차항

g(x)=∫{ x²+ƒ(x) }Δx 가 이차함수일때

x²+ƒ(x)=일차함수

이때 ƒ(x)=-x²+α

 

 

합성함수의 최고차항

ƒ(ƒ(x)) = ∫{ ƒ'(x)-2x }Δx

좌변 ƒ(ƒ(x))의 최고차항은 두 ƒ(x)의 지수곱인 n²

우변에서 적분에 의해 최고 차항은 n-1+1 혹은 1

n²=n을 만족하는 n은 1 즉 ƒ(x)는 1차함수

 

 

적분을 상수항 취급

mx+n=2x-F(t)

이때 F(t)는 상수이므로

m=2 , n=-F(t)

 

 

[심화]

 

수열에대한 적분식

 

 

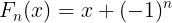
아래첨자 n의 값에 따라서 정적분의 값은 수열의 순서에 따라서

C₁=-1 , C₂=1로 등의 변화 있을 수 있습니다.

 

 

재귀함수에 의한 함수변형

 

 

위의 귀납적 점화식 함수에서 상수항 C는 언제나 1이라고 가정한다면

F₁(x)= (x²/2)+x+1  

F₂=(x³/2·3)+x/2+1 

F₃=(x⁴/2·3·4)+(x³/2·3)+x/2+1 

 

※재귀 함수란 코딩 용어로써 내부에서 자기 자신을 사용하는 함수를 뜻합니다.