[미분] 도함수 그래프와 극값

 

---

1.개념

 

[도함수의 그래프]

 

도함수는 오직 x=0에 대해서 더 큰가 작은가로 살펴보면 쉽게 해석할 수 있습니다.

 

1.증가함수

 

 

도함수를 그래프로 그렸을때 위와같은 모습을 지녔다고 생각해봅시다.

그래프의 모든 구간에서 기울기가 0이 되는 구간이 존재하지 않습니다.

그러므로 그래프는 증가함수 일 것입니다.

 

또한 도함수 그래프의 모양이 2차함수 이므로

미분법에 의한 계산을 생각해보면 원래의 함수는 3차함수가 될 것입니다.

 

기울기가 가파르게 0을 향해서 떨어지는 구간은 점점 수평이 되어가는 구간

기울기가 0에서 가파르게 멀어지는 구간은 점점 수직이 되어가는 구간이므로

 

 

이를 토대로 그래프 개형을 그린다면 함수를 그려본다면 이와 같습니다.

 

만약 도함수가 x축에 접하다면

그래프 중심의 한 점에서만 기울기가 0이 존재하는 증가/감소함수가 됩니다.

 

주의할 점이 있습니다.

미분법에 의해서 ƒ'(x)는 상수항이 사라지기 때문에

이 그래프가 x축이나 y축으로 어느만큼 평행이동 했는가는

도함수 그래프로 추론할 수 없습니다.

 

감소 함수는 따로 그리지 않겠습니다.

 

 

2.도함수의 절대값 그래프

 

 

미분이 불가능한 조건중에 하나는 첨점이 존재하는 것입니다.

다만 그것은 함수를 미분하기 위한 조건일 뿐,

미분 결과가 첨점이 존재해선 안된다는 의미가 아닙니다.

 

물론 이에 대한 이계도함수는 구할 수 없을 것입니다.

 

 

기울기가 서서히 수평에 가까워 지다가

다시 수직에 가까워지는 모습이므로 

그래프 개형은 위의 증가함수와 비슷합니다. 

 

---

[극대와 극소]

 

1.x를 통과하는 도함수

 

 

x의 위쪽은 위를 향해 올라가고

x의 아래쪽은 아래를 향해 떨어집니다.

그래서 도함수가 x를 통과한 다면 원래 함수의 모양은 다음과 같습니다.

 

①위에서 아래로 x축을 통과 했을떄

 

위를 향해 올라가던 그래프가 서서히 수평이 됩니다.

수평해진뒤 아래를 향해 서서히 떨어집니다.

 

②아래에서 위로 x축을 통과했을때

 

아래를 향해 떨어지던 그래프가 서서히 수평이 됩니다.

수평해진뒤 위를 향해 서서히 상승합니다.

 

 

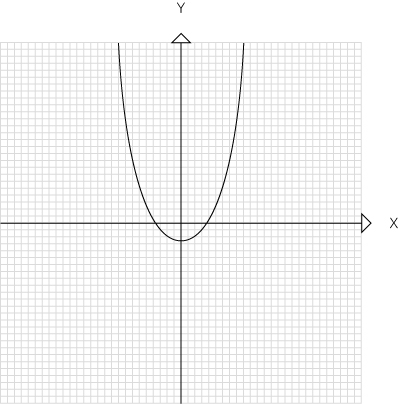
이를 토대로 그래프 개형을 그려보면 파인 모양의 그래프가 됩니다.

 

---

2.극대와 극소

 

 

극댓값과 극소값 : 다차함수에서 기울기가 반전되는 구간을 극점 이라고하며

그중 아래를 향햐는 극값을 극소 , 위를 향하는 극값은 극대 라고 합니다.

 

위의 도함수 그래프에서 봤던 그대로 

ƒ'(x)=0에 해당하는 값은 극값이 됩니다. 

 

변곡점이라는 말은 극점과 다른 의미이므로 (극점 사이의 평균점)

단어 사용에 주의해야 합니다.

 

---

3.극값의 특징

 

①

1차함수를 제외한 홀수 함수에서 극값은 반드시 2개 이상입니다.

도함수에서 x에 접하는 n중근 함수는 증가나 감소함소가 되기 때문입니다.

 

②

극대의 다음 차례는 극소거나 혹은 없으며 이 반대도 적용됩니다.  

이렇게 연속한 두 극값은 극대a>극소b 가 됩니다.

단, 건너뛰는 다음 극값과 비교할때 극소d>극대a 가 될수도 있습니다.

 

③

연속한 함수의 최대 최소값은 지정한 범위의 양 끝이거나 극값이 됩니다.

 

④

극값은 ƒ'(x)=0 에서 성립 하므로 극점은 도함수의 근을 의미합니다.

 

---

4.증감표

 

 

도함수의 근을 중심으로 원함수의 모양을 추측한 표 입니다.

 

ƒ(x)= ⅓x³+ ½x² -6x +1 에 대해서 증감표를 작성하면

다음과 같습니다.

x	…	2	…	-3	…
ƒ'(x)	-	0	-	0	-
ƒ(x)	↗		↘		↗

 

만약 극점이 극대인지 극소인지 모르겠다면

최고차항이 양수일때 떨어지고 시작하는지 (짝수함수)

올라가며 시작하는지 (홀수함수) 보고 판단합니다.

 

---

2.응용

 

[확장지식]

 

1.두 그래프의 ƒ(x)>g(x) 범위

 

①식이 완전히 주어졌다면

ƒ(x)-g(x)>0으로 넘겨서 합친 식에 대하여 최대 최소를 구합니다.

 

②ƒ(x)가 홀수함수 g(x)가 일차함수 라면 

1차함수는 홀수함수를 반드시 관통 때문에 >0이 될수 없습니다.

만약 ƒ(x)가 짝수함수라면. 판별식 D<0 를 사용합니다.

 

③그 외의 경우

f(x)의 최소값>g(x) 최대값

이경우 x지점에 한해서는 g(x)의 최대값을 구할 수 있습니다.

 

만약 그래프 전체에 대하여 이를 적용할 경우

그래프가 톱니처럼 맞물려서 엇갈린다면

ƒ(x)의 최소값 이상에서도 f(x)>g(x)를 만족할 경우가 존재합니다. 

 

 

---

역함수의 조건과 증가감소

역함수가 존재하기 위해선 1대1 함수여야 하므로 원함수가 증가 혹은 감소함수여야 합니다. 

반대로 말해서 역함수는 증가 혹은 감소함수 입니다.

 

 

범위내의 부등식

ƒ(x)>0 가 1<x<3 범위에서 성립한다면 

ƒ(3), ƒ(1), 극값ƒ(a) 중에 가장 작은값 k에 대해서 k>0 로 변형됩니다.

 

 

범위밖의 부등식

1<x<2에서 증가라면 ƒ'(x)≥0이므로 ƒ'(1)≥0 

 

1은 1<x<2 의 범위를 벗어난 존재 임에도

ƒ'(1)≥0 가 성립하는 점이 포인트입니다.

도함수가 존재하려면 연속하고 첨점이 없어야하므로

이 부등식이 반드시 성립할 수 밖에 없습니다.

 

 

상승하는 범위의 추정

ƒ'(x)=-3(x+4)(x-2)≥0

도함수가 최고차항이 음수의 이차함수 이므로 원래 함수는 떨어지는 함수 입니다.

도함수에 ≥0를 임의로 추가하면 상승범위를 추정할 수 있습니다.

→ (x+4)(x-2)≤0 

→ -4≤x≤2 의 범위에서 ƒ(x)는 상승중인 함수

→ 음의 3차함수가 -4≤x≤2 에서 상승일때 ƒ'(x)의 두 근은 -4,2

 

 

---

[기본]

 

범위내의 최대 최소

도함수 : V'(x)=4(x-2)(3x-20) , 범위 : 5≥x≥0

V'(x)=0 일때 극값이므로

부등호내에서 V가 최대최소가 되는 x 의 값은 2

끝값은 V(0),V(5) 가 됩니다.

 

 

기함수의 극값대칭

삼차함수가 x=1에서 극값을 지니고 원점대칭이라면 x=-1에서 극값이 대칭을 이루므로 

도함수는 ƒ'(x)=a(x+1)(x-1) 를 만족합니다.

 

---

[풀이]

 

합성함수의 최대 최소

식 : f'(x)=(t+2)(t-2) , 범위 : -1<t<3

에서 이라면 t는 ±2에서 극값을 지닙니다. 

t=x-1 일때 x-1=2 이므로 x=3에서 극값을 지닙니다.

 

 

삼차함수의 증가

모든 실수에서 증가하려면 x가 음수일때도 ƒ'(x)는 언제나 양수를 유지해야 합니다.

즉 , 기울기가 0이 되는 지점이 존재하지 않거나 1개만 존재해야 하므로

도함수에 대해서 D≤0 입니다. (증가는 한점에서 기울기0일때를 포함합니다.)