[함수의 극한 完] 연속과 연속의정리

 

다른 단원처럼 방정식 부등식 최대최소 그래프가 없는 관계로 단원이 일찍 끝납니다.

더불어서 이전의 다른 단원들과 달리 실생활 예제도 없습니다.

다음 과목의 기초 지식 과목정도이기 때문입니다.

 

연속과 관련해서도 추상적인 개념이 문제가 되는 부분이 있습니다.

깊게 생각하지 않는것을 추천합니다.

이에 대해서는 아래에서 후술합니다.

---

[함수의 연속]

※문구로 설명하자니 개념 자체에 문제가 있어서 일단 그림으로 판단해주시길 바랍니다.

 

1.연속

 

 

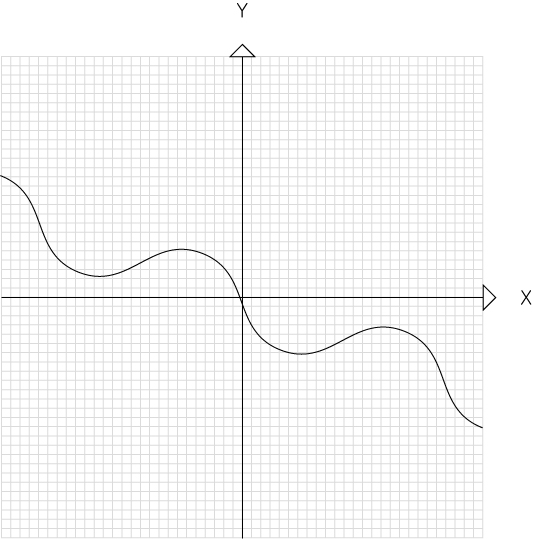
사전적인 정의로만 설명합니다.

모든 구역에서 좌극한=x=우극한을 만족하는 함수 입니다.

연속에대한 개념은 치역(결과값)에만 적용하기 때문에

정의역(대입값)에서만 불연속한 함수는 연속함수입니다.

 

---

2.불연속

 

 

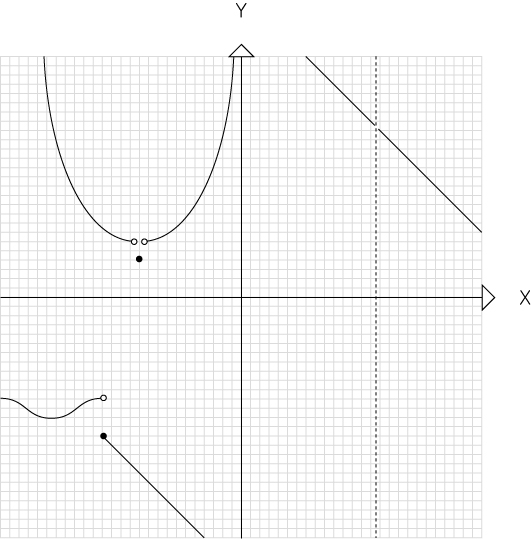
사전적 정의로는

어느 구간에서 좌극한=a=우극한을 만족하지 못하는 함수입니다.

 

오른쪽 위에 점근선이 존재하는 일차함수 그래프는

정의역이 아니라 치역에 대해서 연속인 것이 아닌가 라고 할수 있습니다만,

 

비유를 하자면 {1,2,3} 요소에서

2를 빼고 {1,3}사이만큼의 차이가 존재하므로 연속하지 않는다고

 

당장은 그렇게 이해 해둡시다.

반례 :

작자는 연속이라고 생각합니다.
 A : 1.999999… 와 B : 2.000000… 사이에
인간이 인지하지 못하는 극미한 차이인 Δ 만큼의 차이가 존재한다면
결국 A와 B사이의 차이는 연속하는 수와 다를바가 없기 때문입니다.

다만, 연속을 위와 같은 개념으로 이해해 버릴 경우
일반적인 연속함수와 점근선 함수는 서로 차이점이 없어지기 때문에.
그래프 상에서 점근선이라는 개념이 존재할 수 없게됩니다.

그래서 점근선에 대해서는 포인트를 집어서 예외를 두고
여기에 이것이 있다라는 별도의 설명이 필요한 것입니다.

예를들어 x=2에서 점근선을 지닐때
x=2에 대해서 함수가 불연속 하다라고 말입니다.

---

3.열린구간과 닫힌구간

a<x≤b 일때 (a,b] 라고 표현할 수 있습니다.

그래프에서 특정한 x의 범위를 지정할때 쓰는 개념입니다.

 

만약 하나의 닫힌구간 [a,b]에서 연속 이라고 한다면

a와 b는 각각 좌극한과 우극한 값의 존재는 신경쓰지 않습니다.

즉, a는 a⁺=a , b⁻=b 나머지구간은 x⁻=x=x⁺일때 닫힌 구간에서 연속한다고 합니다.

 

---

3.함수의 연속범위 {암기}

그래프를 그렸을때 연속의 범위는 다음과 같습니다.

 

① 지수,다항,상수함수 = (-∞,∞)

② 무리함수=[k,∞)

③ 유리함수=(-∞,p),(p,∞)

 

---

4.연속하는 두 함수간의 성질

열린구간 (a,b) 에 대해서 연속한 두 함수 ƒ(x),g(x) 간의 연산결과는

열린구간 (a,b) 에서 다음을 만족합니다.

 

① ƒ(x)±g(x) : 연속

② ƒ(x)×g(x) : 연속

③ ƒ(x)÷g(x) : {g(x)≠0} 에 대한 연속

④ (-∞,∞)에 대하여 f∘g, g∘f는 연속

 

단, 반대로 적용해선 안됩니다. ƒ(x)/g(x)가 연속일때

ƒ(x)는 연속 , g(x)는 연속 으로 판단할 수 없습니다.

 

---

5.연속의 추상적인 문제

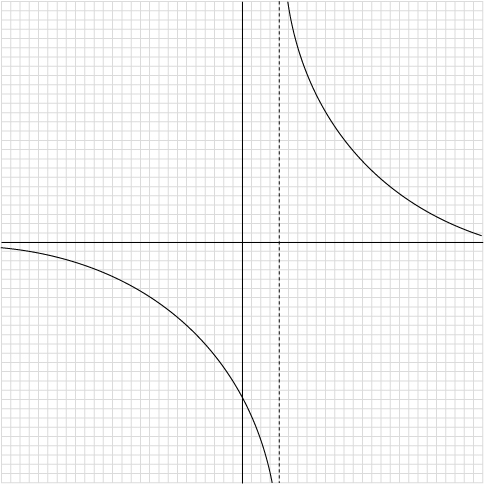
분수함수(유리함수) 입니다.
앞서 말했듯이 연속의 기준은 정의역 x 가 아니라 y입니다.

만약 1/(x-3) 에서 x=3일때 분모가 0이 되는경우,
x에 대한 y값이 존재하지 않습니다, 

이때 x=3은 정의역의 항목에 존재하지 않는 수라고 할 수 있습니다.
x=3이라는 값이 없는 나머지 모든 정의역 안에서 연속이기 때문에
분수함수는 연속함수입니다.

한편으로는 이렇게 생각할 수 있습니다.
그 지점 한개가 사라진다고 해도 그 지점하나를 제외한 그래프가
한쪽은 위를 향하고 한쪽은 아래를 향하는데 이게 어떻게 연속이냐는 겁니다.

여기에서 그 이유가 굉장히 추상적입니다.
입실론 델타증명 은 과정을 넘어가니 생략하고

분수함수의 위 아래의 무한대의 어느 한 지점을 인간이 생각하기에 끝지점이라고 생각한다면,
과연 그보다 더 큰 값이 없겠느냐는 문제입니다.
어느 지점이 끝이라고 주장을 한다고해도 그보다 더 크거나 작은수는 반드시 존재하고
그렇기 때문에 끝이란게 존재하지 않습니다.
그것이 분수함수가 연속함수로 취급되는 이유입니다.

여기에서 한가지 문제가 발생합니다.
위의 두 관점을 기준으로 분수함수를 연속함수로 분류 했다면.

1/x가 x=0에서 불연속이라 라는 표현이 과연 옳은가? 입니다.
앞으로 연속에 대한 문제를 풀게된다면,
정의역에 x=0이란게 없는데도,
유리함수가 x=0에서 불연속이라 하는 여러 문제들을 보게 될 겁니다.

잘못된 쪽은 어디일까요?
분수함수를 연속함수라고 주장하는 쪽일까요
아니면 x=0에서 불연속이라고 주장하는 쪽일까요

극한과 마찬가지로 연속또한 이런 개념적 마찰이 존재합니다.
그래서 작자는 개념적으로 깊히 생각하지 말것을 권고합니다.

※만약에 위와같은 그래프의 치역이 무한이 아닌 정해져 있는 수렴하는 숫자 (ex: 2,-2)라면
이 때는 좌극한 혹은 우극한이없는 불연속 함수로 간주됩니다. 

 

---

[연속의 정리]

※아래의 정리들은 분수함수의 특정 구역을 제외합니다.

 

1.최대최소 정리

 

닫힌구간 [a,b] 에서 연속한다면 최대 최소값이 존재합니다.

만약 열린 구간 (a,b)일 경우

위의 그래프에선 b)에서 최소값이 존재하지 않는다고 정의합니다.

 

---

2.사잇값 정리

 

 

ƒ(a)≠ƒ(b), [a,b] 에서 연속한다면

ƒ(a)<ƒ(c)<ƒ(b)를 만족하는 x=c값이 [a,b] 내부에 존재합니다.

 

---

3.샌드위치 정리

 

limƒ(x)=L , limg(x)=L , ƒ(x)≤h(x)≤g(x) 라고할때

h(x)=L로 정의합니다.

 

---

3.기타 정리

 

limƒ(x)=L , limg(x)=M , ƒ(x)<g(x) 일때 L≤M

1/(x+1) < 1/x일때 x→∞ 를 대입한다면 0=0로 취급됩니다.

 

---

2.응용

[추가 지식]

1.2차식의 분수함수는 점근선이 2개

이차분수함수는 1/{(x-1)(x-3)}에 대하여

(-∞~1),(1~3),(3~∞)의 연속의 구간을 지닙니다.

 

2.f(x)의 연속의 반례
전에 언급한 적이 있습니다.

혹은 가우스, 갯수 그래프를 이용하기도 합니다.

 

3.합성함수에 의해 불연속이 연속으로 변경
g(x)가 x=0에서 불연속이라 할지라도 내부값으로 f(x)를 대입했을때 

x=0에서 연속을 만족하여 연속이될수도 있습니다.

 

 

4.불연속 함수를 곱했을 때의 좌우 극한 
f(x)g(x)가 연속이여야할때

f(x)가 x=a에 대하여 불연속이라면 f(x)의 좌우 극한값에 대해서

f(x)g(x)가 연속하기위해선 예시로 2*g(a)=0*g(a) 와같이 나타 낼수 있습니다. 
이때 2와 0에 어떤 숫자를 곱해도 항등하기위한 g(a)=0 밖에 없으며 

그렇다면 이때 g(x)=Q(x)(x-a)라고 할수 있습니다.

 

 

5.연립 방정식의 연속과 해의 관계

연립 방정식 식A=식B 에서 오직 x=k에서만 연속한다면

두 f(x)식이 x=k에서 한점에서 만난다고 할수도 있습니다. (판별식D=0) 

 

 

6.사잇값 정리에 의한 근의 범위 추정

 

①근의 범위 추정

연속하는 함수 ƒ(x)가 ƒ(0)=-3, ƒ(1)=-3, ƒ(2)=7 라고 할때

ƒ(c)=0의 구간이 ƒ(1)<ƒ(c)<ƒ(2) 이므로 실근은 (1,2) 의 범위 안에 있습니다.

 

②교점의 범위 추정

함수A=함수B의 연립식을 ƒ(x)라고 둘때

ƒ(a)ƒ(b)<0 가 성립한다면 (a,b)의 구간에서 적어도 하나의 교점을 지닙니다.

 

③임의의 근의 위치를 두기 위한 상수항의 허용범위

(-2,3)에서 실근을 지니기위해선 ƒ(-2)ƒ(3)<0 가 만족해야 합니다.

ƒ(x) = {x+a} 의 함수를 대입해보면 (a-2)(a+3)<0 가 되므로

-3<a<2 의 a의 범위를 구할 수 있습니다.

 

---

[기본]

 

1.무리수의 닫힌구간
√(9-x²) 에서 닫힌 구간의 정의역은 [-3,3] 가 됩니다.

범위를 벗어날 경우 허수가 되기 때문입니다.

 

2.2x+1=0에서 x=-1/2 가 점근선
1 / (2x+1)일때 -1/2에대한 점근선이 있다고 판단하여

연속의구간은 (-∞,-½),(-½,∞)입니다.

 

3.절대값의 불연속
ƒ(x)=1 / |x-1| 는 1에서 좌극한과 우극한의 값이 다른 식이므로 불연속함수 입니다.

 

4.조건함수가 연속할 조건

ƒ(x)={x<a : x²-2, x≥a : x}

좌우 극한을 대입해서 a⁺→a , a⁻→a²-2 일때

x=a 에서 연속하기위해선 a=a²-2 가 만족해야 하므로

이를 만족하는 a의 값은 -1 또는 2입니다.

 

---

 

[풀이]

 

1.가우스기호의 좌우극한
ƒ(x) =[x]²+3[x]a 가 x=-2에서 연속일때

우극한=4+6a 좌극한=1+3a

즉 , 4+6a=1+3a 이므로

연속하기 위한 a의 값은 -1입니다. 

 

 

2.불연속을 혼합한 식의 연속확인

g(x) = {x>a : f(x)+c , x≤a : x²+c} 이며 x=a에서 연속, 

f(x)가 x=b에서 불연속 이라면 
⑴ x→a g(x)를 파악 

⑵ x→b g(x)를 파악.

만약 둘다 극한이 같다면 이때 이 함수는 해당구간에서 연속입니다.

 

---

[사잇 값의 실생활 적용]

어떤 사람이 정지해있다가 10km/h로 뛰기 시작하는 지점사이의 어느한 시간엔
5km로 뛰는 구간이 존재합니다.

 

---

함수의 극한 完