[수열 完] 점화식 수열과 귀납법

 

+2022-11-28 잘못 작성된 이미지 수정

---

1.개념

 

[점화식 수열]

 

1.점화식

 

 

수열이 지니고 있는 항들사이에 존재하는 관계 식 입니다.

모든 수열들에서 만족하는 식 뿐만이 아닌,

특정 수열에서만 만족하는 항들 사이의 등차,등비 관계식을 포함합니다.

 

---

2.점화식 수열

 

 

이전항과 다음항의 연산으로 이루어지는 수열입니다.

위의 예제에 있는 파보나치 수열은 점화식 수열의 종류 중에 하나입니다.

 

---

3.점화식 일반항

 

점화식 수열에서도 등비 등차에 대한 별개의 이름은 존재하지 않지만,

이전항 다음항을 사용하는 일반적인 등차,등비수열은 아래와 같이 정리됩니다.

 

①점화식 등차수열

 

 

②점화식 등비수열

 

 

---

[귀납적 수열]

 

1.귀납적 정의

 

일반항으로 표현할수 없는 수열을 나타내기위해서

이웃하는 항들간의 관계를 정의 하는 것을 의미합니다.

점화식이 수열의 공통적인 관계나 단순한 등차와 등비의 관계를 의미한다면,

귀납적 정의는 그 외의 항들간의 다른 연산들을 포함하는 더 넓은 개념입니다. 

 

---

2.귀납적 수열

 

 

귀납적 수열은 정의되어있는 수열들 외에 규칙이 존재하는 기타 미분류 수열들에 해당됩니다.

그래서 표현식에 따라서 등비/등차수열의 개념을 벗어난 수열이 될수도 있습니다.

이것이 규칙이 없는 난수들의 묶음을 의미하는 것은 아닙니다.

 

---

3.귀납적 일반항

귀납적 수열도 등비수열과 등차수열을 만족하는 경우

이를 대략적인 ƒ(n)혹은 ƒ(aₓ)로 표현하면 a+ƒ(n) 혹은 a·ƒ(n)로 표현됩니다. 

 

---

[수학적 귀납법]

 

1.개념
공식이지닌 미지수에 1,2,3를 대입하는 축차대입법에 대하여 연속되어 참인가를 증명하는 방법입니다.

귀납적 점화식 수열 , 점화식 수열에 대해서 일반항을 가정했다면 맞는지 확인하기 위해서 사용됩니다.

 

귀납법의 흐름

① n=1,n=2,n=3이 참이라는 것을 확인

② a₁, a₂에의한 a₃의참이 성립을 확인

③ 그렇다면 a₂, a₃에 의하여 a₄는 참이라고 추측

④ 이 후의 모든 항에 대하여 성립한다고 가정합니다.

 

즉 , 귀납법의 증명에 필요한 최소조건은 3개입니다.

 

---

2.증명

 

귀납법에 의한 증명은 흐름을 암기하는 과정입니다.

아래 예제에서 전체적인 흐름을 이해해 봅시다.

진행 도중에 좌우변에 더하는 값은

방정식인가 부등식인가에 따라서 생각보다 정형화 되어있습니다.

 

방정식 증명

 

논제 :

1·2 + 2·3 … n(n+1) = ⅓n(n+1)(n+2) 이 참인가?

 

첫째항 증명 : 

n=1일때 참 ★

 

첫째항의 참에 의한 가정 : 

n=k가 참이므로 1*2…+k(k+1) = ⅓k(k+1)(k+2)

 

연속하는 다른 항의 증명 : 

n=k+1도 참인가 ? 

방정식의 좌우변 양끝에 +(k+1)(k+2) 
→1*2…+n(n+1) + (k+1)(k+2) = ⅓k(k+1)(k+2) + 3*⅓(k+1)(k+2)

 

이때 ⅓k(k+1)(k+2) + 3*⅓(k+1)(k+2) = ⅓(k+1)(k+2)(k+3) 을 만족한다.

즉, 이는 n=k+1을 대입한 식과 동일하므로 식이 충족한다.

 

그러므로 최소조건 첫째항 1 , 중간항 k , 다음항 k+1 3개가 참이 되므로

수학적 귀납법에 의해 식은 참이다.

 

---

부등식 증명

※입력의 한계로 인해 주황색n은 상수를 의미하고 있습니다.

 

논제 :

(1+h)ⁿ>1+nh (n≥2 , h≥0) 이 참인가? 

 

첫째항 증명 : 

n=2일때 참 ★

첫째항의 참에 의한 가정 :  

n=n가 참이므로 (1+h)ⁿ>1+nh

 

연속하는 다른 항의 증명  : 

n=n+1도 참인가 ?

방정식의 좌우변 양끝에 ×(1+h)
→(1+h)ⁿ(1+h)>1+nh(1+h)

 

이때 1+nh(1+h) = 1+(k+1)h+kh² 이며 

이는 1+(k+1)h 보다 kh² 만큼 크다. 

그러므로 (1+h)ⁿ⁺¹ > () > 1+(k+1)h 가 성립.

 

그러므로 최소조건 첫째항 1 , 중간항n , 다음항n+1 3개가 참이 되므로

수학적 귀납법에 의해 식은 참이다.

 

---

[수열 합의 실사용]

 

정규 과정에서 따로 언급이 존재합니다.

다만, 아래 두줄로 요약됩니다.

 

1.복리이자를 포함 매년 말에 갚는다 할때 

 

 

 

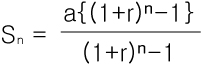
2.복리이자를 포함 매년 초에 저축한다고 할때 

 

 

---

수열 完