[미분] 미분계수와 도함수

 

앞으로 진행하는 내용들은 함수의 극한을 알고 있다는 전제로 진행합니다.

 

작자가 미분과정에서 일부분 전달하지 않는 지식이 있습니다.

기본적으로 필요한 지식들과 과정들은 전부 작성합니다.

알려주지 않는 부분에 대한 것은 단원이 끝날때 조금의 소개로 이유를 알려드리겠습니다.

 

이번 글은 확장 지식 항목이 없고 기본에 예시 풀이가 추가되어있습니다.

앞으로 미분 사용에 있어서 기본적으로 반드시 알아야 하는 정보들이기 때문입니다.

---

1.개념

 

[미분계수]

 

1.평균변화율

 

 

그래프 위의 두 점에 대해서

중2 과정에서 배웠던 기울기를 구하는 방법을 사용해서

두 점 사이의 평균 기울기를 구할 수 있습니다. 이를 평균변화율이라고 합니다.

 

※요약하자면 두 점의 각 지점을 (x₁,y₁) 과 (x₂,y₂) 라고 할 때

이 두점 사이의 기울기는 (y₂-y₁)/(x₂-x₁) 라는 내용이였습니다.

 

---

2.미분계수

 

 

그래프가 지니고있는 어느 한 점이 지니고있는 순간적인 기울기를

미분계수 혹은 순간변화율 이라고 합니다.

그래프 위의 지정한 지점에 대해서

인간이 인지하지 못하는 점의 양끝 사이의 평균변화율인 dy/dx 입니다.

혹은 d 대신에 인간이 인지하지 못할만큼 작은수 Δ(델타,h→0)를 사용하기도 합니다.  

※d는 미분을 뜻하는 영단어의 줄임말입니다.

 

---

[도함수]

 

1.정의

 

 

ƒ(x) 에 대해서 그래프 위의 한 점의 좌표를 (x,ƒ(x)) 라고 생각해봅시다.

만약 x 지점에 대해서 미분계수를 구한다면 그 결과는 하나의 식이 나옵니다.

이 때의 식을 도함수 라고 하며 ƒ'(x) 로 표기합니다.

※에프 프라임 엑스 라고 읽습니다.

 

그래프 를 그리기 위해서 y=ax+b 의 형식으로 도함수를 표현한다면

이에 대해선 y'=ax+b로 표현합니다.

 

도함수에 대해서 추가로 도함수를 겹쳐서 구할수 있습니다.

이때의 도함수는 이계도함수 라고 하며 f"(x)로 표현합니다.

 

---

2.도함수의 식

 

 

평균 변화율 식을 순간 변화율과 착각해서 ƒ'(x)로 취급하지 않게 주의가 필요합니다.

몇몇 경우에서 평균 변화율의 식이 도함수와 똑같아 져서 ƒ'(x)로 취급할 수 있는 경우가 있는데,

이는 아래 추가지식에서 다룹니다.

 

---

3.미분의 조건

 

①좌미분계수 ≒ 우미분계수
②연속한 함수이며 그래프가 급격히 변화하는 첨점이 없을 것
③정의에 의해서 미분계수가 분명히 존재하는 경우

ex) g'(x)={x＝0 : f(0) , x≠0 : k}

 

---

4.미분법

 

미분을 더 쉽게하는 방법입니다.

모든 항에서 지수를 1 내리고 지수만큼 계수에 곱한뒤 상수항을 제거합니다.

예를 들어서 2x³은 2x²로 내린뒤에 3·2x²로 마무리해줍니다.

ex)y = x³-3x²+1 → y' = 3x²-6x

 

만약 xƒ(x) 같이 x 곱해진 수에의해서 차수가 변동될 가능성이 있다면

먼저 x를 식에 풀어준 뒤에 계산을 해야합니다.

ƒ(x)의 식을 모르기 때문에 건드릴 수 없다면

아래에 후술한 성질에 의해서 미분을 진행합니다.

 

---

5.도함수 변형의 성질 {암기}

① y = ƒ(x)±g(x)

→ y' = ƒ'(x)±g'(x)

 

② y = ƒ(x)g(x)h(x)

→ y'=ƒ'(x)g(x)h(x)+ƒ(x)g'(x)h(x)+ƒ(x)g(x)h'(x)

 

③ y = ƒ∘g(x)

→ ƒ'∘g(x)g'(x)

 

④ y = kƒ(x)

→ kƒ'(x)

※단 , k≠x 일것

 

⑤ y = ƒ(x)³

→ 3ƒ(x)ƒ'(x)

※2번 식과 같습니다.

 

⑥ ƒ(x) = ƒ(-x)(y축대칭)

→ ƒ'(x) = -ƒ'(-x)

 

---

2.응용

[기본]

 

1.기본적인 미분

f(x)=3x+1 의 f(2)미분

 

 

3Δx+7-7/Δx = 3

※상수항은 반드시 제거됩니다.

 

 

2.극한식 대입에 의한 미분 성립

 

 

x가 0에 한없이 가까운 숫자일때 f(x)/x 결과는 Δy/Δx 를 만족하므로 미분식이 됩니다.

 

 

3.평균변화율이 도함수가 되는 경우

 

 

만약 lim(x→1)에서 ƒ(x-1)/x , ƒ(0)=0 이라면 {ƒ(x-1)-ƒ(0)} / {x-0} 에서

Δy/Δx 를 만족하므로 미분식이 됩니다.

 

4.도함수에 의한 차수 추정

 

①

ƒ'(x)=x+ƒ(0) 일때 ƒ(0)는 0을 대입한 결과값 숫자이므로 상수

x+c 는 일차함수 이므로 도함수에 대한 원래함수는 이차함수입니다.

②

ƒ'(x){ƒ'(x)}=f(x)

f'(X)의 차수는 f(x)과 비교해 n-1가 되어야 하며 두 도함수의 곱으로 최고차항은 xⁿ·xⁿ

즉 , (n-1)+(n-1) = n 의 식을 만족하는 n의 값은 2 입니다.

 

③
ƒ(x)ƒ'(x)=x⁵+C 이때 ƒ(x)의 차수가 n일때 지수는 n+(n-1)=5 가 되므로  n은 3 입니다.

 

5.인수분해식의 미분

(x-3)(2x-1)

→f'(x)= (x-3)'(2x-1)+(x-3)(2x-1)' = (1)(2x-1)+(x-3)(2)  

 

6.제곱식의 미분

(3x-2)⁴ 

→f'(x)=4(3x-2)³(3x-2)' = (3x-2)³(12)

 

7.미분의 조건

ƒ(x)={ x≥2 : x² , x<2 : ax+b} 일때 미분가능하려면 

①좌극한=우극한(2a+b=4) 

②좌미분=우미분(a=4)

 

 

8.델타(h,Δ)의 차이

 

 

 

---

 

[필수]

 

 

a.함수차를 임의로 추가하기 

 

 

 

 

= 2ƒ'(x)-3ƒ'(x) 

 

 

b.ƒ(n)=0 일때 임의 추가하기

ƒ(x)/(x-3) , ƒ(3)=0 

→

 

 

---

[풀이]

 

 

1.외부의 식 조건
ƒ(x+y)=ƒ(x)+ƒ(y) , 

→ƒ(0)=ƒ(0)+ƒ(0)을 만족해야하므로 ƒ(0)=0

 

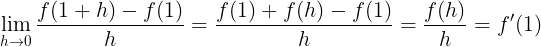
위의 ƒ(x+y)=ƒ(x)+ƒ(y)에 의해서 분리됩니다.

0에 대한 미분도 분자에서 ±ƒ(0) 에 의해서 ƒ(h)만 남게 되므로 ƒ'(0)=ƒ(1)입니다.

 

 

2.도함수를 상수함수 취급
ƒ(x)=2x²+3xƒ'(1)

→ ƒ'(1)는 상수(결과값) 이므로 a로 취급 
→ ƒ'(x)=4x+3a , ƒ'(1)=4+3a = a  ∴ a=-2

 

 

3.dy/dx는 미분식

 

 

→ ƒ'(x)=ax+3-3Δx ,

Δ→0 이므로

ƒ'(x)=ax+3

 

---

[테크닉]

 

1.분모의 계수는 임의 조정이 가능합니다.

 

 

 

 

2.±ƒ(x)를 임의 추가

 

 

= 2ƒ'(2)-ƒ(2) 

 

-ƒ(2)가 성립하는 이유는

-xƒ(2) 와 +2ƒ(2)를 ƒ(2)로 묶어서 -(x-2)를 약분했기 때문입니다.

 

 

3.분모 곱의 교환

 

 

 

 

4.미분역수

 

 

 

 

5.부분적으로 함수로 묶기

 

 

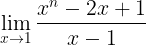
xⁿ-2x 를 f(x)라고 가정합니다.

ƒ(x)에 1을 대입한 ƒ(1)=-1 이므로

f(x)+1 은 f(x)-f(1)로 변형됩니다.

이때 식의 정리 결과는 ƒ'(1)가 됩니다.