집합의 함수

1.함수의 영역

 

①함수와 집합의 관계

 

 

f(x)=2x (혹은 y=2x) 라는 함수가 있다고 해봅시다.

여기에서 x를 자연수들의 집합이라고 가정했을때

집합 X 안에있는 요소들에 f(x)를 적용하면 2의 배수가 될 것입니다.

즉, 함수란 X라는 집합안의 요소들을 Y의 요소로 바꾸는 식이라고 할 수 있습니다.

f : X→Y

이를 줄여서 글씨로 표현하면 위와 같으며,

X의 모든원소 x는 f에 의해 Y의 어느 요소들에 대응된다 라고 읽습니다.

 

이때 한 요소 x에 대응되는 y가 여러개이거나

x중에 y에 대응하지 않는 요소가 존재한다면 둘은 함수관계가 성립되지 않습니다.

 

이를 조건 제시법으로 표현하면

Y = {(x,y)|y=f(x),x∈X} 로 표현됩니다.

 

함수를 집합의 개념으로 보았을때 가정에 의한 함수도 존재할 수 있습니다.

예를 들면 진리집합X =  x보다 작은 양의 소수들로 만드는 함수f(x) 라고 정의가 가능합니다.

---

②함수와 집합의 구성

 

 

함수 f 에 대입되는 x의 범위를 f의 정의역 이라고 합니다.

함수 Y' 안의 요소들 중에서 f에 의해서 x와 대응하는 영역을 f의 치역 이라고 합니다.

치역을 포함한 모든 집합 Y의 영역을 f의 공역/공변역 이라고 합니다.

 

함수의 종류에 따라서 정의역의 범위는 다음과 같습니다.

 

1. 분수함수(유리함수) : 분모가 0이아닌 수의 집합 
2. 무리함수 : √내부의 숫자가 0이상의 양수인 수의 집합 
3. 로그함수 : x진수가 최소 0 초과인 수.

 

로그함수는 고2에서 배우므로 지금은 대강 정의역의 영역에 대한 감만 잡으시면 됩니다.

 

만약 같은 정의역 X에 대하여 함수 f , g 의 치역이 같다면 이때 f(x)=g(x)라고 합니다.

함수식을 풀어서 등식으로 푼뒤 0에대한 정리가 가능해집니다. 

---

③f의 분류

 

1)단사함수(일대일 함수)

 

 

대응하지 않는 나머지를 제외한 Y의 값들에 1대 1로 대응하는 함수입니다.

즉 , f(2)=f(1) 같은 결과값이 서로 겹침이 없는 함수를 의미합니다.

 

2)전단사함수(일대일 대응)

 

 

Y의 모든 요소가 X에 1대1로 대응하여 공역=치역인 상태의 함수입니다.

치역 = 공역일 때 반드시 전단사 함수를 만족하진 않습니다.

정의역과 치역의 갯수가 반드시 같습니다.

 

그래프상에서 1대1로 대응한다는 것은 1차함수처럼 x당 y의 해가 1개라는 뜻이기도 합니다.

이를 응용한다면 y=x²도 x>0라는 조건을 붙힌다면  1대1로 대응하여 전단사함수가 됩니다.

 

3)항등함수

 

 

f(x)=x+1 이라면 집합X의 요소의 갯수가 무한대일때

집합Y의 요소의 갯수도 똑같이 무한대가 됩니다.

즉, X에 1,2,3,4 가 존재할때 Y에도 1,2,3,4가 존재할 것이며

음수까지 끝없이 이어지는 숫자들 사이에서 모든 요소들을 비교해보면

집합 X와 집합 Y가 같은 요소들로 이루어져 있을 것입니다.

 

이렇게 함수 f를 사용하기 전후의 집합의 요소들이 변화가 없을때

이 함수를 항등함수 라고 합니다.

항등함수는 줄여서 대문자 아이 I 로 표기 됩니다.

 

 

항등함수는 함수의 적용 전후의 집합의 내용물의 변화가 없는 것을 의미합니다.

즉 , 함수 결과만 만족된다면 단사함수처럼 공역과 치역이 다를 수 있습니다.

그러나 항등함수는 특히 여러 연산곱에 중요하게 사용되는 개념이기 때문에

사용상 편의를 위해서 반드시 치역=공역 인것으로 임의로 정의 되어있습니다.

즉, 위의 그림은 정의에 따라서 항등함수가 아닙니다.

 

4)상수함수

 

 

어떤 x 값을 대입해도 같은 결과를 지닌 함수를 상수함수라고 합니다.

 

5)역함수

 

 

역함수란 f : X → Y 가 성립할때 다시 Y → X 로 되돌리는 함수를 의미합니다.

역함수의 본래의 함수를 원함수 라고 합니다.

지수로 -1 이라 표현되며 역함수와 원함수는 정의역과 치역이 서로 반전됩니다.

그러므로 역함수가 존재하기 위해선 공역=치역 일 필요가있습니다.

 

 

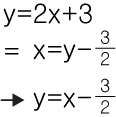
역함수는 y에 대한 식을 x에 대한 식으로 정리한뒤 x와 y의 자리를 바꿔서 구할 수 있습니다.

그래서 원함수의 그래프 위에  (x,y) 가 있다면 역함수가  (y,x)를 지나간다는 특성이 있습니다.

그래서 역함수의 그래프는 원함수를 y=x에 대하여 대칭한 모양을 지닙니다.

역함수의 역함수는 다시 원함수로 돌아갑니다.

 

 

x와 y의 자리가 바뀐다는 특성으로 함수 상으로 위와 같이 변형해서 쓸수 있습니다.

이때 원함수와 역함수는 필요충분조건을 지닌다고 할수도 있습니다.

f(3)=f(x+1) 일때 f(x)가 자기자신에게로의 역함수가 존재한다면 3=x+1로 풀어어서 쓸수 있습니다.

 

역함수=원함수(f(f(x))=x) 일 경우도 있습니다. 이때 그래프 상으로 두 함수는 y=x에 대한 대칭을 이룹니다.

이는 다시 말해서 원함수와 역함수의 교점이 y=x 위에 존재한다는 뜻입니다.

그래서 만약 역함수=원함수 라면 y=x 와 연립방정식을 진행해서 교점을 구할 수 있습니다.

또는 f(5)=1 일때 그래프상 (5,1)의 좌표를 지나가므로 역함수는 (1,5)를 지나간다고 할 수 있습니다.

 

---

④함수의 갯수

 

이하에서 말하는 모든 Y의 값들은 서로 다릅니다.

 

1)전단사

전단사함수를 만족하는 함수의 갯수는 x의 원소가 5개일때 

5x4x3x2x1(경우의수) 의 갯수를 지니게 됩니다.

 

X에 5개의 요소가 있을때 y도 5개있을 것입니다.

함수를 통해서 숫자1의 자리가 Y의 첫번째자리,두번째자리,세번째자리~ 로 대응할 수 있다면,

이때 경우의 수는 5개, 정해진 한 자리를 제외하고 4개 3개 2개... 그래서 위의 계산이 나옵니다.

 

즉, 여기에서 함수의 갯수란 같은 결과 Y가 나오는 모든 함수들은 하나로 취급하여 계산됩니다.

 

2)단사

단사함수의 갯수는 전단사에서 n(X) 갯수 만큼만 곱합니다.

X={1,2,3} , n(Y)=4 일대

1이 가리킬수있는 숫자는 4개

2가 가리킬수있는 숫자는 3개

3이 가리킬수있는 숫자는 2개이므로

 

갯수는 4x3x2 가 됩니다.

 

3)전체

X→Y를 만족하는 모든 함수의 총갯수는 m =  n(Y), n = n(X)라고 할때 mⁿ 이됩니다.

 

X={1,2,3} , Y={1,2,3,4} 라고 했을때

1은 Y의 1,2,3,4에 대응할 수 있습니다.

2는 Y의 1,2,3,4에 대응할 수 있으며 겹치는 것이 가능합니다.

3은 Y의 1,2,3,4에 대응할 수 있으며 겹치는 것이 가능합니다.

 

그러면 경우의 수는 4 x 4 x 4 가되며 이는 mⁿ 과 같아집니다.

 

4)상수함수

상수함수의 갯수는 n(Y) 가 됩니다.

 

5)치역=공역

치역=공역인 함수의 갯수는 

n(X)≥n(Y) 임을 전제로 진행 합니다.

전체 함수의 갯수 - 원소1개가 대응하지않는 함수 전체의 갯수 ꞏꞏꞏ - n-1개가 대응하지않는 함수 전체의 갯수

고1에서 배우는 과정이라기보단 현재로썬 이런 것이 있다는 개념만 알고 넘어가는 정보입니다.추후에 순열과 조합 과목에서 풀이하겠습니다.

 

---

⑤합성함수

 

g∘f 혹은 (g∘f)(x) = g(f(x))

즉 , 함수안에 함수가 들어가있는 상태를 의미합니다.

또한 이때 f(x)의 치역은 g(x)의 정의역이 될 것입니다.

g(x)=x+3 이라고 할때 f(g(x)) 는 f(x+3) 으로 작성해서 쓸수도 있습니다.

 

x값을 대입할때 풀이의 순서는 g∘f 일때 f(x)를 먼저 구한다음 그 결과값을 g(x)에 대입합니다.

그래서 g∘f 에 대해서 교환법칙은 성립하지 않습니다.

그러나 만약 교환법칙이 성립된다면 g∘f 는 항등식 일 것입니다.

③-3)에서 설명한 항등함수는 함수를 적용했을때 자기자신이 나옵니다.

그래서 f∘I = i∘f = f 가 성립할 것입니다.

 

 

합성함수는 역함수에 대해서 서로 묶거나 분리할 수 있습니다.

-1이 제곱의 의미로 사용되는 것이 아니기 때문입니다.

 

1)합성함수의 그래프 개형

 

이 내용의 세부사항은 고1 과정의 내용이 아닙니다.

다만 어디까지나 감을 잡는 정도의 간단한 내용은 존재합니다.

 

⑴포물선의 합성함수

 

f(x)가 v의 형태를 띄고 있을때 자기자신의 함성함수 그래프는 포물선의 갯수가 제곱됩니다.

 

⑵일직선의 합성함수

 

 

f(x)는 g(x)가 지니고있는 y값들 중에서 g(x)와 겹치는값이 1 하나밖에 없습니다.

그러므로 이 둘의 함성함수는 y=1 이 됩니다.

g(f(x)) 임에 주의해야 합니다.

 

⑵증가/감소함수

 

 

증가함수에서 g(x) 그래프의 모습을 붉은 영역내로 축소해서 그린 모습이 됩니다.

감소함수에서 g(x) 그래프의 모습을 좌우 대칭해서 푸른 영역내로 그린 모습이 됩니다.

g(f(x)) 임에 주의해야 합니다.

 

---

2.응용

 

A1)합성함수의 추측

 

 

만약 (f∘h)(x) 의 결과가 g(x)와 같다면

이때 h 의 역활은 f(x)로 변형된 집합 X를 역함수로 되돌리고 함수 g(x)를 대입한다고 할수 있습니다.

 

A2)부등식 집합과 y의 범위

 

 

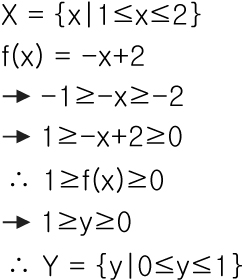
A3)미지수와 역함수

 

 

A4)미지수와 자기자신의 함수

 

 

A5)합성함수의 역계산

 

 

g(f(x)) 와 (g∘f)(x)의 식이 같아야 하므로 둘은 항등식이 됩니다.

 

A6)모든 함수에 성립한다.

함수 f가 모든 함수 g에 대하여 성립한다는 말을 풀어서 식으로 쓰면

g(f(x)) = g(x) 를 의미하며 이때  f(x)는 항등함수 I입니다.

 

A7)괄호식 정리

 

 

A8)항등함수가 아닐결우

 

 

f(5)=5 라고할때 즉 f(x)=x 를 만족했을때

이는 f(x)의 그래프와 y=x의 그래프의 교점이라고 할 수 있습니다.

그러므로 f(5)=5를 만족했을때 이 함수를 항등함수라고 할 수 없습니다.