-
1.증명의 방법
①명제/조건/부정
3>2
명제 : 그것이 참인지 거짓인지 확실히 알수 있는 식이나 문단
3>2 는 참인 것을 알 수있는 명제입니다. 2>3은 거짓인 것을 알 수있는 명제입니다.
명제가 거짓이라면 부정은 항상 참이라고 간주됩니다.
명제가 참이라면 부정은 항상 거짓이됩니다.
p : x>2
조건 : 판명이 가능하지만 환경과 변화에 따라서 참과 거짓이 변하는 식이나 문단.
x-2=0 일때 x 의 값에 따라서 참일수도 거짓일수도 있으므로 조건에 해당합니다.
식이나 문단에 p,q,r 순으로 이름을 붙혀서 사용할 수 있습니다.
~p : x≤2
부정 : 조건이나 명제를 ≠ 처럼 부정형으로 뒤집어 사용하는 것을 의미합니다.
조건 p 가 있을때 ~p 로 작성하며
명제는 단순히 수식의 조건을 반대로 뒤집어서 거짓으로 만들어줍니다.
부정은 진리집합P에 대해서 P의여집합의 값을 지니게 됩니다.
~(~p) = p 가 됩니다.
⑴
p : x>0 일때 조건이 참이 되게하는 모든 x의 집합 {1,0.5,√2 ···} 을 진리집합이라고 합니다.
조건의 이름이 p 일때 진리집합은 대문자 P 로 표현됩니다.
⑵
조건의 상황에 따라 진리집합은 집합간의 법칙에 영향을 받습니다.
p또는 q 일때 진리집합은 P∪Q 가 됩니다.
p이고 q 일때 진리집합은 P∩Q 가 됩니다.
⑶

⑷
진리집합의 여집합을 만족하는 조건과조건의 관계를 서로 부정형 이라고 합니다.
ex) 모든 정수에 대해서 x>0 ↔ 모든 정수에 대해서 x≤0
②조건의 관계
p→q : p가참일때 q도 참이 됩니다.
위에서 p 는 가정 , q 는 결론 이라고 합니다.
x가 4의 약수일때 x는 8의 약수라는 조건이 참이 됩니다.
즉 , 참이 되기 위해선 4의 약수를 P, 8의 약수를 Q 라고하면 p→q 일때 P⊂Q를 만족해야 합니다.
반대로 말해서 P⊂Q 일때 p→q 라고 할수도 있습니다.
x가 2의 배수일때 x는 4의 배수이다 라고할때 거짓이 됩니다.
6,10,14 등은 4의 배수가 아니이기 때문입니다. 이렇게 참을 부정하는 증거들을 반례 라고합니다.
반례에 대해서 p→q 기호에 ≠ 같은 부정형은 존재하지 않습니다.
그냥 거짓 이라고 결론을 말합니다.
1)확정된 명제
p ⇒ q
p→q 가 참이라는 것이 확실해져서 명제라고 할수 있을때 화살표를 위와같이 작성합니다.
여기에서 참이라는 것이 확실하다의 의미는 P⊂Q 를 만족한다 는 뜻입니다.
(아래가 헷갈린다면 P를 내용물 , Q를 상자 라고 생각해봅시다.)
이때 p는 q이기 위한 (q를 증명하는데에 성공한) 충분조건,
q는 p에 대한 (q를 증명하는데에 필요한) 필요조건.
p⇔q
혹은 p⇔q 일때 필요충분조건 혹은 서로 동치한다고 합니다.
서로 동치할때 P=Q 를 만족하며, 둘이 지니고 있는 요소가 같으므로
Q∈P, P∈Q를 충족합니다.
다음 두 식에 대한 필요충분조건을 만족합니다.
a²+b²=0 ⇔ a=b=0 a>b ⇔ √a>√b (a,b는 양수) 2)역
p → q 의 역 : q → p
역이 Q⊂P 을 만족하지 않을 경우 역은 거짓이 될 것입니다.
3)대우
p → q 의 대우 : ~q→~p
p→q가 명제일때 ~q→~p도 같이 참이 됩니다.
p→q가 거짓일때 ~q→~p도 같이 거짓이 됩니다.
ex. 명제 : x=2 이면 x+2=4이다. 대우 : x+2≠4 이면 x≠2 이다.
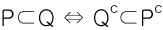
진리집합으로는 위의 조건을 충족한다고 할 수 있습니다.
4)이
p → q 의 이 : ~p → ~q
이는 역과 대우이기 때문에 역과 참과 거짓을 공유합니다.
명제가 참일때 이는 거짓이 됩니다.
③증명법
1)직접증명법
참이라 인정되는 몇개의 명제들로 추론을 계속하여 명제가 참인지 증명합니다.
ex)
p : 0은 짝수이다. (조건)
q: 2로 나누어 떨어지면 짝수다(명제)
p→q :
2로 나누었을때 결과를 0으로 만드는 모든 숫자들의 집합 U에대하여
분수 0/2 는 2조각중에 조각이 없음을 뜻해서 0으로 취급 된다.
이때 몱은 0이므로 P⊂Q 이며 p⇒q
⑵삼단논법
p⇒q ,q⇒r 그러므로 p⇒r
집합단원에서 A⊂B , B⊂C 일때 A⊂C 라고 표현한 것과 같습니다.
주로 본래의 명제보단 대우들의 삼단논법을 활용합니다.
조건이 아니라 명제들로만 성립하므로 주의해야합니다.
2)간접증명법
조건을 직접 증명하지 않고 대우의 참이나 부정의 거짓을 증명합니다.
ex)
~p : 0은 홀수다
~q: 홀수일때 2로 나누어 떨어지지 않는다.(명제)
~p→~q :
분수 0/2 는 0으로 취급 되므로 나누어 떨어집니다.
0은 ~q에 대해서 거짓이므로 홀수가 아닙니다.
더보기사실 0 은 짝수도 홀수도 아닌 독립된 개체로 취급됩니다.
하지만 여러 짝수의 개념과 함께 사용되기 편하므로 짝수성 을 지닌다 라고 표현합니다.
하므로 경우에 따라선 짝수로 취급할 때도 , 아닐 때도 있는 수입니다.명제를 부정하여 증명하는 방법을 귀류법 이라고 합니다.
2.절대부등식
x에 어떤 허수 i 가 아닌 모든 수를 대입해도 대소관계가 항상 참을 만족하는 부등식입니다.
보통 실수라고 표현하는데 그렇다고 음수를 무시하는 것도 아니며, 등식도 포함됩니다.
1)예시표
⑴기초적인 대소관계
a²≥0 |a|≥a |a|²=a² |ab|=|a||b| |a÷b|=|a|÷|b| ⑵인수분해 정리에 따른 증명
|a|+|b|≥|a+b| |a+b| 에서 a와 b의 부호가 다르다면 숫자의 폭은 더 줄어들 것입니다. |a|-|b|≤|a-b| 제곱해서 정리하면 2(ab-|a||b|) 가 되며 |a||b|=|ab|≥ab 이므로 ≤0가 성립합니다. a²±ab+b² ≥ 0 (복부호동순) (a±1/2b)²+3/4b² 으로 정리되므로 음수가 나올 수 없습니다. a²+b²+c²-ab-bc-ca ≥ 0 1/2{(a-b)²+(b-c)²+(c-a)²} 으로 정리되므로 음수가 나올 수 없습니다. 2)산술평균과 기하평균
(a+b)/2≥√ab
기하평균이란 직사각형과 같은 넓이를 가진 정사각형의 한변의 길이를 뜻합니다.
(a+b)/2-√ab = (√a-√b)²/2가 되므로 항상 ≥ 0를 성립합니다.
이 부등식만 따로 작성한 이유는 양변에 2를 곱했을 때,
a+b≥2√ab 로 정리되기 때문입니다. 다른말로하면 a+b의 최소값은 2√ab 라고 표현되기도 합니다.
단 , 인수분해식에는 적용할 수 없습니다.
예를 들어 (a+b)(c+d)의 최소값을 구한다고 할때 (√ab)(√cd) 로 정리해서 쓸 수는 없습니다.
3.응용
A1)모든 , 어떤
모든 x에 대하여 p를 만족한다면 P=U 일때 참이라고 할수 있습니다. 모든 x는 U를 뜻하기 때문입니다.
어떤 x에 대하여 p를 만족한다면 P≠Ø 일때 참이라고 할수 있습니다. U의 요소 중 하나라도 충족하는가를 뜻합니다.
모든 ↔ 어떤
ex) 모든 실수에 대해 x≠1 이다 (거짓) ↔ 어떤 실수에 대해서 x≠1 이다 (참).
이때 참인가 거짓인가는 반례가 존재하는가 아닌가로 판단합니다.
A2)조건제시법 내부의 또는
Q = {x|조건1 또는 조건2} 라고 할때 진리집합 P₁를 조건1 , P₂를 조건2라고 취급하여
P₁UP₂⊂Q 를 만족하는 진리집합을 구합니다.
A3)절댓값
절댓값 식의 조건을 증명할땐 양변을 제곱해서 절댓값을 제거한뒤 진행할 수 있습니다.
A4)
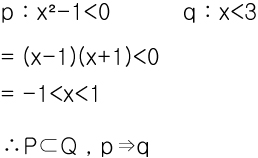
A5)대우에의한 조건제시법

B는 3의 배수 의외의 모든 정수를 뜻합니다.
이 때 B의 대우는 3의 배수중에 3의 거듭제곱이 아닌 모든 수를 뜻합니다.
'수학 > 고1' 카테고리의 다른 글
무리함수와 유리함수의 그래프 (0) 2022.06.20 집합의 함수 (0) 2022.06.19 집합 (0) 2022.06.14 단원 외의 간단한 개념들2 (0) 2022.06.12 수학의 말장난2 (0) 2022.06.12