-
1.좌표평면의 구성요소

- x축 : 방향의 기준으로 사용하기 위해서 수평으로 그은 직선입니다.
- y축 : 방향의 기준으로 사용하기 위해서 수직으로 그은 직선입니다.
- 사분면 : x축과 y축의 경계로 생긴 구역들 입니다.
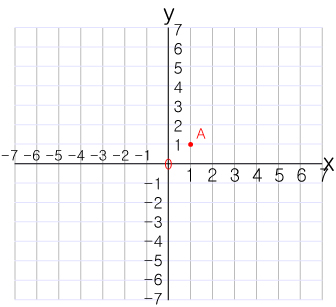
x 축과 x 축의 거리별로 숫자로 표현한다면 양수와 음수로 표현됩니다.
어느 위치에 점 A 가 있다고 할 때,
이것을 A(1,1) 이라고 표기하여 점 A 의 정확한 위치를 파악할 수 있습니다.
이것을 좌표 라고합니다.
1.5 순서쌍
만약에 A가 x축 기준으로 2 , 4 , 6 중에 하나에 있고 y축 기준으로 3 , 5 , 7 중에 하나에 있다고 해봅시다.
그러면 (2,4,6) 과 (2,5,7) 로 나타날 수 있는 모든 좌표들은
(2,2) , (2,5) , (2,7) , (4,2) , (4,5) , (4,7) , (6,2) , (6,5) , (6,7)
가 있을 것입니다.
이렇게 두 이상의 집단에서 만들어 질수 있는 여러 조합들을 순서쌍 이라고 합니다.
순서쌍의 갯수는 집단의 갯수 x 집단의 갯수 로 구할 수 있습니다.
2.좌표평면의 특징

만약에 좌표 A(x,y) 의값을 A(-x,y) 로 바꾸면 Y축을 기준으로 대칭돼는 방향으로 이동할 것입니다.
그리고 이는 A(x,-y) 로 바꿨을때 X축을 기준으로 대칭돼는 방향으로 이동할 것입니다.
이때 A는 1사분면에서 2사분면으로 , 4사분면으로 이동할 것입니다.
만약 A(-x,-y)의 좌표라면 A 원점(0) 을 기준으로 3사분면으로 이동할 것입니다.
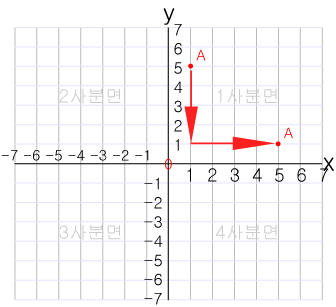
A(a,b) 를 A(b,a) 로 바꾼다면 A 는 대각선을 기준으로 대칭되는 방향으로 이동할 것입니다.
3.좌표이동
x의 값이 작아지면 ←왼쪽으로 커지면 오른쪽→ 으로 이동하는 효과를 볼 수 있습니다.
y의 값이 커지면 ↑위쪽으로 작아지면 ↓아래쪽으로 이동하는 효과를 볼 수 있습니다.
이 개념은 실제로 컴퓨터에서 물체의 이동을 화면에 보일 때 사용하는 개념입니다.

만약에 A(x,y) 에서 x = 1 이고 y = 2 라면
X(x-2y, -x+2y) 만큼 이동하라고 할 수도 있을 것입니다.
이때 이것을 풀면 X(-3,3) 가됩니다.
그러면 1을 -3만큼 움직이므로 x = -2 가 되고 2을 3만큼 움직이므로 y = 5가 될 것입니다.
이때 A(-2,5)는 2사분면에 있다고 할 수 있을 것입니다.
'수학 > 중1' 카테고리의 다른 글
여러가지 선의 표현과 컴퍼스 (0) 2022.03.01 그래프와 비례 (0) 2022.02.28 일차식 이차식 (1) 2022.02.28 비율 응용(short) (0) 2022.02.28 분수의 특징 심화과정 (0) 2022.02.28