-
+2022-11-24 이미 알고 있어야 이해할 수 있는 설명들을 쉽게 해석, 문맥 정리
1.넓이
1)개념
이렇게 다르게 생긴 두 도형 중에서 어떤것이 더 크고 어떤것이 더 작다고 할지 기준을 잡기가 힘들 때가 있습니다.
그래서 이것을 정확한 숫자로 표현하고 어느것이 더 큰지 정확한 비교를 하기 위해서,
혹은 이것이 얼마나 커다란 것인지 정확히 알기 위해서 사용되는 것이 넓이 입니다.
넓이의 비교는 서로의 길이의 단위 비교하는 방법입니다.
예를 들자면,

우리는 이 둘의 길이를 비교해서 어느 것이 더 긴지를 한눈에 예측할 수 있습니다.
그렇다면,

이렇게 선을 뒤로 나열했을 때
6cm 선이 4번 놓인 크기와 7cm선이 3번 놓인 크기라고 파악 할 수 있습니다.
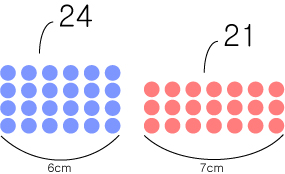
만약에 1cm당 하나의 점으로 표현해 본다면 우리는 점의 갯수를 통해서
6x5의 모양과 7x4의 모양중에 어느 것이 더 큰지를 확인할 수 있습니다.

가로선(누운 선)를 길이로 보고 세로선(서 있는 선)을 갯수로 볼 것인가 ,
세로를 길이로 보고 가로를 갯수로 볼 것인가 ,
7x3 이 되었건 , 3x7이 되었건 둘의 결과는 같겠죠?
다시말해서 , 가로와 세로를 둘다 갯수로 생각하건,
가로와 세로를 둘다 길이로 생각하건 결과는 같다는 것입니다.
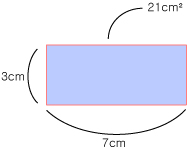
그렇다는 말은 이렇게 길이 x 길이 를 사용해서 한 면의 넓이를 표현할수 있다는 뜻입니다..
이때, 이 사각형의 넓이는 7x3 인 21이 되는 것이고, cm x cm 로만들어졌다는 뜻으로
이것을 제곱센티미터(cm²) 라고 합니다. 즉 이 사각형의 넓이는 21cm² 입니다.

이렇게 숫자를 통해서 넓이를 구해놨으니,
이제 두 면 중에서 어느쪽이 더 큰지 알수 있게 되었습니다.
2)각종 도형의 넓이
①사각형

직사각형 과 정사각형의 넓이는 가로(누운 선 방향) x 세로(서 있는 선 방향)를 통해서 구할 수 있습니다.
여기에서 아래쪽 가로선을 밑변 , 세로선을 높이 라고 합니다.
②삼각형
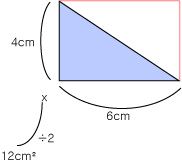
삼각형은 사각형을 반을 자른 형태라고도 할 수 있습니다.
그래서 삼각형의 넓이는 밑변×높이 ÷ 2 라고 구할 수 있습니다.

삼각형은 형태와 상관없이 밑변의 길이하고 높이만 같다면 넓이가 같다는 특징이 있습니다.
③마름모

사각형을 반으로 잘라서 삼각형을 만들었을 때
그 삼각형 4개를 서로 이어붙여서 위의 그림같은 형태를 만들었다면 이 형태를 마름모 라고 합니다.
마름모의 넓이는 가장 긴 가로 길이와 가장 긴 세로 길이를 서로 곱한뒤에 ÷ 2 를 해서 넓이를 구할 수 있습니다.
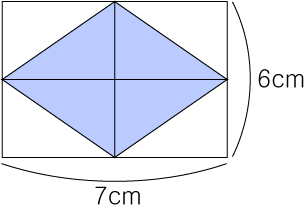
그림과 같이 가장긴 가로선과 가장 긴 세로선으로 밑변과 높이를 만들어서 사각형을 만들어 보면
사각형과 비교해봤을 때 마름모 안에 들어있는 삼각형의 갯수는 반만 있다는 것을 알 수 있습니다.
그래서 ÷ 2 를 하는 것입니다.
④사다리꼴
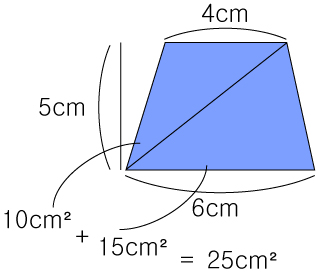
사다리꼴의 넓이는 그림과 같이 두개의 삼각형의 의 넓이를 서로 더한 값이라고 생각할 수 있습니다.
두개의 삼각형은 사다리꼴의 모서리를 서로 선으로 이어서 만듭니다.
즉 , 윗변의 길이 x 높이 ÷ 2
+ 아랫변의 길이 x 높이 ÷ 2
3.넓이의 단위를 변경하기
아까 설명한대로 넓이의 단위로는 cm² 가 쓰입니다.
그렇다면, 이것을 m²(제곱미터) 이라고도 쓰고,
mm²(제곱미리미터) 라고도 쓰고,
km²(제곱키로미터) 라고도 쓸 수 있겠지요.
만약에 cm x m 의 크기를 가진다면,
이럴 땐 m 를 cm 로 내리거나 (1m는 100cm 입니다.)
cm 를 m 로 올려서 사용합니다. (100cm 는 1m 입니다.)
만약에 1m x 1m 크기의 정사각형이 있다면 이것은 1m² 의 넓이를 가질 것입니다.

1m 는 100cm 니까 이를 바꿔서 표현하면 아래와 같습니다.

즉, 1m² = 10000cm² 라는 것을 알 수 있습니다.
1km² 도 똑같이 1000m x 1000m 의 크기일 것입니다.
그래서 1km² = 1000,000m² 이라는 사실을 알 수 있습니다.
2.둘레
1.개념
둘레는 면을 구성하는 모든 윗변,아랫변,옆변들의 길이를 합친 것 입니다.

넓이가 클수록 둘레도 커집니다.
하지만 둘레는 넓이처럼 크기의 비교에 사용하기엔 정확하지 않습니다.
그래서 둘레는 물체를 만들때 재료가 얼마나 필요한지 추측하기 위해서 사용 되거나
어떤 물체의 주위를 걸어다닐 때 얼마나 걸어야 하는지 알기 위해서 사용됩니다.
예외적으로 크기의 비교에 사용되는 경우도 있습니다.
옷을 입을 때 옷의 치수를 확인하는 것이 이에 해당합니다.
2.둘레의 특징
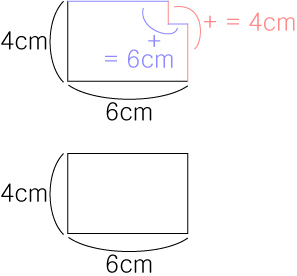
직사각형이나 정사각형의 모서리가 직각으로 파였을 때와 파이지 않았을 때
서로의 둘레의 길이를 재보면 똑같다는 특징이있습니다.
모서리가 아닌 부위에서 파였을 때 파인 부위 만큼 둘레의 길이는 증가합니다.
'수학 > 초5' 카테고리의 다른 글
대각선 (short) (0) 2022.02.15 직육면체와 평면도 (short) (0) 2022.02.15 소수의 사칙연산 (short) (0) 2022.02.13 분수와 소수의 관계 (0) 2022.02.12 통분과 분수의 크기 비교 (short) (0) 2022.02.11