회전, 내각, 외각 의 특징

https://mytory.tistory.com/31

각도와 형태

 

 

지난번에는 각도가 무엇인지 간략하게만 알아봤습니다.

이번엔 각종 각도들의 특징들을 살펴봅시다.

 

각도 관련 부분들은 주로 모형 설계에서 사용됩니다.

---

1. 회전각

 

이번엔 각도를 선과 선 사이의 이동 거리라고 생각해봅시다.

 

 

그렇다고 하면은 90°(구십도) 만큼 한번더 이동해서

 

 

이렇게 눕혀진 거리까지의 각도를 90° + 90° 니까 180° 라고 할 수 있지 않을까요?

 

 

그렇다는 것은 선이 90° 씩 이동할 때마다 90°, 180°, 270°, 360° 만큼 회전했다 하고 할 수 있을 것입니다.

그림에서 볼 수 있듯이, 360° 를 돌면 결국 0° 의 장소로 돌아오게됩니다.

그래서 한 바퀴를 나타내는 총 각도는 360° 입니다.

주의할 점은, 0° 와 360° 의 모양은 같지만 의미가 완전히 같다고 할 수는 없습니다.

0° 는 조금도 움직이지 않았다 는 뜻이고, 360° 는 한바퀴를 돌고 왔다는 뜻입니다.

즉, 공간의 개념이 아니라 시간의 개념으로 본다면 둘을 별개로 생각하는 것이 좋습니다,

 

그렇다면 이것을 응용해 봅시다.

 

 

이 노란 별을 왼쪽으로 180도 만큼 이동한다면 별의 모양은 어떻게 될까요?

 

 

별이 뒤집혔습니다.

회전의 각도는 물체를 상하좌우로 반전(뒤집는것)시킬때도 사용되는 개념입니다.

---

2. 내각 과 외각

 

 

위와 같이 도형이 있을 때 도형의 안쪽에있는 각을 내각,

도형의 바깥에있는 각은 외각 이라고 합니다.

이때 외각은 내각과 합쳤을때 180° 여야 한다는 기준으로 그려집니다.

위 그림의 사각형에는 내각이 4개 있다 라고 볼 수 있습니다.

 

 

다음 과같이 삼각형이 존재할 때,

 

 

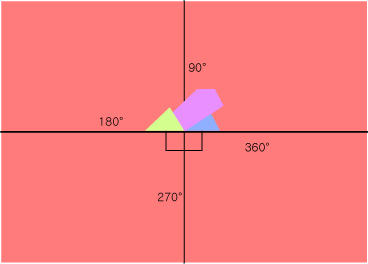
삼각형을 잘라서 모든 내각을 합치면 총 180° 가 됩니다.

이는 삼각형을 어떤 모양으로 그려도 같은 결과가 나옵니다.

 

사각형도 마찬가지입니다. 사각형의 모든 내각을 합치면 총 360° 만이 나옵니다.

---

3. 다각형의 내각

 

오각형을 넘는 도형들을 다각형 이라고 합니다.

삼각형의 내각의 합이 180°

사각형의 내각의 합이 360°

 

그러면 오각형 , 육각형, 칠각형 전부 외워야 될까요?

 

좀더 간단한 방법이 있습니다.

 

 

여기에 오각형이 있습니다. 오각형의 내각의 합이 알고 싶은 상황입니다.

 

 

그러면 아무 꼭지점 하나에 모든 꼭지점들을 이어봅시다.

 

 

그러면 보았을 때 삼각형이 3개가 생기는 것을 볼수 있습니다.

삼각형 1개의 내각의 합은 180° 라고했습니다.

3개의 삼각형을 합치면 정답은 180° x 3 인 540° 가 됩니다.

하므로 오각형의 내각의 합은 540° 입니다.

 

이것을 그림을 그리지 않고 숫자로만 표현하면

?각형일때 ? - 2 를 한뒤 x 180° 를 하면 내각의 합을 구할수 있다고 할 수 있습니다.

 

그림의 이해를 해봅시다.

 

 

 

이 빨간 지점의 각도는

 

 

초록 지점의 내각 + 파란 지점의 내각 하고 같을 것입니다.

 

 

그리고 이런 사실은 위에있는 각도 또한 같을 것입니다.

 

 

모두 칠해봅시다. 결국 모든 삼각형들의 내각을 더하면 오각형의 내각의 합과 같다는 것을 알 수 있습니다.

그런데 삼각형은 어떻게 그려도 내각의 합이 180° 라고 했습니다.

결국은 오각형의 합은 180° x 3 하고 같다는 것입니다.

---

ex.응용문제

 

 

①

 

사각형의 한 내각이 63° 라고 할때, 외각은 몇도일까요?

 

 

②

 

그렇다면 그림처럼 외각이 2개 있다고 했을 때 초록색 지점의 각도는 몇도일까요?

 

 

③

 

이 그림에서 빨간색 지점의 각도는 몇도일까요?

 

④

 

 

이 도형의 내각의 합은 얼마일까요?