더하기와 빼기

https://mytory.tistory.com/18?category=987784 

숫자를 사용하고 읽는 여러가지 방법

이 글은 다음 글을 숙지했다고 가정하여 진행합니다.

---

1.더하기 / 덧셈 / 합

 

다음 그림을 보고 원의 갯수가 몇개인지 맞춰봅시다.

 

 

이렇게 보는 원의 갯수는 한눈에 바로 알아차리기 힘듭니다.

훈련하지 않은 인간이 한 눈에 인지할 수 있는 갯수는 5~7개라는 한계가 있기 때문입니다.

그렇다면 이 원을 이렇게 정렬해보는 것은 어떨까요?

 

 

그리고 이것을 아랫 방향으로 한줄 씩 읽어봅시다.

 

 

우리는 원들을 일일히 세어보면서 이 원들의 총 갯수가 9개 라는 것을 이미 알고 있습니다.

여기에서 우리는 위의 그림을 아래의 표현으로 바꿀 수 있을 것입니다.

 

 

 

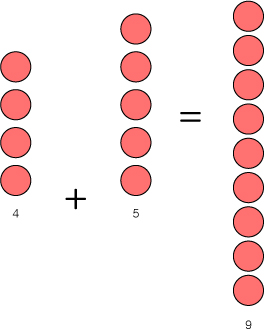
= 이란 ? 

= 의 왼쪽(←) 과 오른쪽(→) 의 물체들의 갯수를 각각 세어봤을 때 , 똑같은 숫자가 나온다 는 뜻입니다.

 

+ 란?

+ 의 왼쪽(←) 과 오른쪽(→) 의 물체들의 갯수를 전부 모아서 세어보라는 뜻입니다.

4+5 자체가 하나의 묶인 단위 생각해본다면 4+5 = 9 라고 할 수도 있겠지요.

우리는 이것을 더하기 라고 합니다.

 

더하기를 통해 합이 10이 넘어가는 것은 초1의 과정을 넘어서기 때문에 다음에 다시 다루겠습니다.

 

---

1.빼기 / 뺄셈 / 차

 

앞서 살펴본 9개 원을 사과로 생각하고 봅시다.

처음에 9개 였던 사과들 중에서 몇개의 사과가 썩었습니다.

 

 

그리고 이때 세어보니, 썩은 사과의 갯수가 4개 있습니다.

그리고 이 썩은 사과들을 모두 버리면 남는 사과는 몇개일까요?

 

 

이렇게 사과는 5개가 남았습니다.

이것을 빼기(-)라고 합니다.

 

위의 내용을 정리하면, '9개의 사과 에서 4개의 썩은 사과를 빼면 5개가 남는다' 입니다.

그리고 이것을 덧셈 처럼 간단 하게 적어서,

9 - 4 = 5 라고 적을 수 있습니다.

 

덧셈과는 다르게 뺄셈은 무조건!  숫자들을 오른쪽(→) 으로 읽어가며 풀어야 합니다.

 

5 + 4 = 9 이고

4 + 5 = 9 이므로 덧셈은 순서가 상관이 없지만

 

9 - 4 = 5 의 경우

9가 원래 있던 사과의 갯수 , 4는 썩어버린 사과의 갯수로 생각하는 것 이고,

4 - 9 = ? 의 경우

4는 원래 있던 사과의 갯수 9는 썩어버린 사과의 갯수라는 의미가 되기 때문입니다.

 

위의 4-9=? 의 정답이 무엇인지는 초1의 범위를 벗어나기 때문에

지금은 개념만 생각하고 추후에 다시 보겠습니다.

---

번외 : 덧셈 과 뺄셈을 읽는 방법

 

2 + 3 = 5 

이 더하기 삼 은 오

이 와 삼의 합은 오

 

3 - 1 = 2

삼 빼기 일 은 이

삼 과 일의 차는 이

 

모든 더하는 행위들을 통틀어서 덧셈 이라고 합니다.

모든 빼는 행위들을 통틀어서 뺄셈 이라고 합니다.

▷나 요즘 뺄셈에 자신이 붙은 것 같아

 

---

더하기와 빼기는 빠르게 물체의 갯수(외 기타등등)을 파악하거나 예측하는 것에 쓰입니다.

여러 숫자들을 비교해가면서 익숙해지는 연습이 많이 필요하지만,

작성자는 개념에 초점을 두고 있으므로 예시 문제를 제공하진 않겠습니다.