-
도형의 이동과 대칭수학/고1 2022. 6. 11. 22:46
1.도형의 평행이동
1)좌표의 이동

점의 좌표가 (x+9,y) 라고 한다면 이는 점을 오른쪽으로 9만큼 움직이라는 뜻이 됩니다.
2)직선의 이동
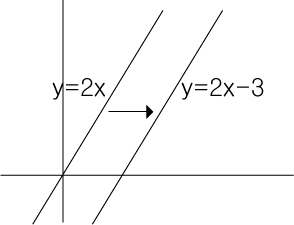
상수항이 y 절편과 같으므로
상수항이 -3일때 x축으로는 기울기인 2/3만큼 오른쪽으로 이동한 효과가 있습니다.
3)포물선의 이동

3차함수와 직선의 중심도 이에 포함됩니다.
x-2 일때 +2 만큼 움직인다는 점에 주의해야합니다.
4)원의 이동

x,y-2 일때 +2 만큼 움직인다는 점에 주의해야합니다.
2.도형의 대칭이동
1)개념

대칭이동이란 그래프의 꼭지점을 축을 기준으로 이동하는것을 의미합니다.
이 때, 꼭지점의 좌표를 이동하면서 그래프의 모양 또한 축에 대칭된 모양을 지니게 됩니다.
2)x축 대칭이동

3)y축 대칭이동
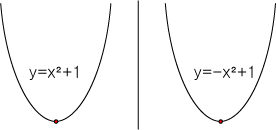
x의 부호를 반전합니다.
이때 y=(x+1)²+1 과 같이 되어있다면
y=(-x+1)²+1 로 바꿔줍니다.
3)x=n 대칭이동
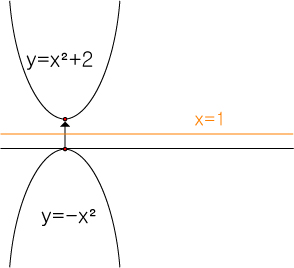
y=-x²의 꼭지점과 x=1 간의 거리는 1 입니다.
그러므로 대칭이동하는 상수항 , 또는 원의 방정식의 (y-n)²의 n값은
거리의 2배를 한 2가 될 것입니다.
y의 부호를 바꾼뒤 상수항이나 (y-n)²의 값을 해당값으로 대체해줍니다.
4)원점에 대한 대칭이동

원점에 대하여 대칭이동한 두 꼭지점 좌표는 합했을때 0이 됩니다.
5)x=y에 대한 대칭이동

6)x=-y에 대한 대칭이동

풀어서 y에 대한 함수식으로 다시 작성해야 합니다.
7)x나 y의 대칭이동

3.평행이동 혹은 대칭이동
1)직선에대한 대칭이동
⑴

(1,2)지점에 꼭지점이 존재하는 도형을 y=2x+3에 대하여 대칭이동하려고 합니다.
꼭지점의 도착지점을 (n,m) 이라고 한다면
이때 점P의 x좌표는 (n+1)/2, y좌표는 (m+1)/2 라고 할수 있습니다.
y=2x+3에 ((n+1)/2,(m+1)/2)을 대입해보면
① (m+1)/2=2((n+1)/2)+3
한편 점 p에대하여 90도 기울기를 지니는 회색 직선 l₂ 의 기울기는
기울기 2를 -1 로 만드는 -1/2가 될 것입니다.
이 직선의 방정식을 y=-½x+k로 두고 지나가는 점인 (1,2)를 대입하면
k=5/2 즉 이 직선의 방정식은 y=-½x+5/2 가 됩니다.
여기에 (n,m)을 대입하면
② m=-½n+5/2
즉, 이렇게 구한 ① 과 ②를 서로 연립해주면 꼭지점이 이동하는 값인 (n,m)을 얻을 수 있습니다.
대칭이동이라면 꼭지점에 대해서 그래프의 기울기가 반전되게 하는 것을 잊지 맙시다.
⑵
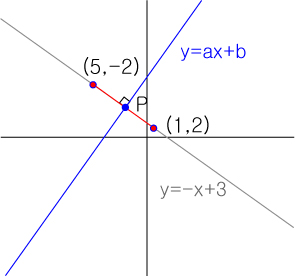
이 방법을 반대로 하면 대칭축을 찾을 수 있습니다.
점 P의 좌표는 ((5+1)/2,(-2+2)/2) 가 되며
(5,-2) , (1,2)를 통해서 두점의 직선의 방정식을 구할 수 있으므로
이에 수직한 기울기를 찾아 점 P의 값을 대입하면 대칭축의 방정식이 될 것입니다.
2)점에대한 대칭이동

꼭지점의 시작 지점을 (x,y) , 끝점을 (a,b)라고 해봅시다.
P의 좌표가(3,0) 이므로 (x+a)/2=3, (y+b)/2=0 이 될 것입니다.
이 식을 변형해보면 a=6-x , b=-y 가 됩니다.
대칭점 P도 a=6-x 일때 P(6/2)=(a+x)/2 이므로 쉽게 구할 수 있습니다.
(n,m) 좌표로 평행이동을 직선의 방정식에 의한 직선의 중심에 적용할때
굳이 함수식으로 정리하지 않고 진행할 수 있습니다.
y=-2/3x+2 → (y-m)-2=2/3(x-n)
2(x-n)+3(y-m)=6 → 3(y-m)-6=2(x-n) → (y-m)-2=2/3(x-n)
둘의 결과가 같음을 알 수 있습니다.
3)미지수 좌표의 대칭이동(다소 어려움)
방정식을 좌표에 대해서 평행이동할땐 y=x 를 y - -x +1 로 변경하는 것 처럼
부호를 바꾸고 예상되는 꼭지점의 위치값을 대입하면 방정식을 대칭이동 할 수 있습니다.
그러나 대칭점 P를 제외한 방정식 위의 임의의 시작 좌표가 미지수라면 이 방식을 쓸수 없는데,
방정식 위의 미지의 좌표에 대한 이동방법은 아래의 방법을 사용합니다.
(x,y)=이동전 원래좌표 , (a,b)=이동 후의 좌표 , P = (x+a)/2
1.a=2P-x → x=2P-a , b=2P-y → y=2P-b
>여기에서 2P 는 a의 좌표와 x의 좌표간의 총합거리라고 할 수 있습니다.
x와 a의 총합거리에서 a를 빼면 x만 남을 것입니다.
2.대칭이동하고자 하는 함수가 y=x² 이라면 (2P-b)=(2P-a)²
3.(2P-b)=(2P-a)²→ (2P-y)=(2P-x)² (a와b를 x와y로 치환)
식을 전개해서 정리하면 평행이동한 그래프의 함수가 됩니다.
예를 들어서 y=(x-2)² 을 2P-b=(2P-a-2)²로 대체했다고 해봅시다.
여기에서 (2P-a-2)의 의미를 해석해보면 (총합거리-새로운미지수대표될(x) - 현재의 x좌표)
그런데 위의 식 정리로 2P-x=a (총합거리 - x좌표 = a의 좌표)란 것을 알았으니까
(총합거리-새로운미지수대표될(x) - 현재의 x좌표)
즉, a를 x로 치환해서 써서 방정식이 성립하는 이유는
결과가 이동된 거리를 표현하는 좌표식과 같아지기 때문입니다.
이를 적용하여 방정식을 이동할때 (2-y)=(2-x)²과 같이 y가 음수가 되는 특성이 있어 대칭이동이 됩니다.
다만 식을 정리할때 (-y-1)² 은 (y+1)² 와 같이 이차식에서 정리하면서 부호는 변경됩니다.(원의 방정식)
4.개념적 이동
1)
직선을 대칭이동 하기 전후가 같다면 대칭점이 직선 위에 존재할 것입니다.
만약 2x+3y=6을 x를n, y를m 만큼 평행이동 해서 방정식이 같다면
2(x-n)+3(y-m)=6 라고할때 2x+3y-(2n+3m)=6 으로 정리한뒤에
방정식을 유지하기 위해선 2n+3m=0 이 되어야 함을 알 수 있습니다.
2)
함수 f(x) , f(x,y)는 평행이동할 때 f(x-1) , f(x-1,y-1) 혹은 -f(x,y)로 적용 가능합니다.
함수의 모양에 상관없이 그 모양은 대칭이 적용됩니다.
4.응용 및 심화
A1)

두개의 교점을 가지는 포물선과 선y=x가 있을때
y=x에 대하여 대칭되는 포물선 위의 점의 좌표입니다.
이때 포물선위의 두 점은 미지수로 (a,b) , (b,a) 라고 표현할 수 있습니다.
a,b 를 구한다면 내용이 주제와 무관하고 복잡합니다. 확인하려면 아래를 클릭해주세요.
더보기y=x²+x 일때 a=b²+b , b=a²+a 가 성립합니다.
연립하면 a-b=a²-b²+a-b , 여기에서 a²-b²+a-a+b-b=0 이 되므로
(a-b)(a+b)=0 이 됩니다.
즉 a+b=0 에 대해서 a=-b 이므로
a=b²+b 에 대입해서 정리해보면 b²+2b=0 이 됩니다.
b(b+2)=0 이므로 이때 b의 값은 0,-2 a또한 0,-2가 나올 것입니다.
a-b=0 에 대해서 b=a²+a 를 대입해보면 a²=0 이 되므로 0은 중근임을 알수 있습니다.
그렇다면 중근을 제외한 -2 를 각각 a=b²+b 와 b=a²+a 에 대입해보면
a=-2 일때 b=2, b=-2일때 a=2 가 성립합니다.
즉, y=x에 대칭을 만족하는 포물선 위의 두 점은 (2,-2) , (-2,2) 입니다.A2)
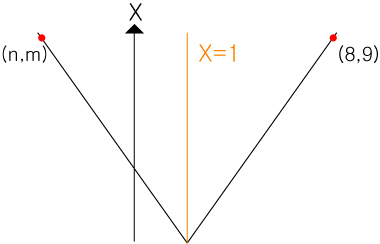
서로 대칭하는 두 직선이 v형을 띈다고 할때
(n,m) 의 값은 (n+8)/2=1 이므로 n=-6이 될것이며 대칭 될때 m은 9가될 것입니다.
두 직선을 직선의 방정식에 따라 각각 y-9=a(x-8) , y-9=-a(x+6) 이라고하며
이때 두직선이 x=1 에서 교점을 지니므로
y-9=a(1-8) , y-9=-a(1+6)에서 서로의 y값은 같을 것입니다.
이때 y+7a=9 y-7a=9 로 정리되며 연립하면 기울기 a를 구할수 있습니다.
A3)

ㄷ자 모양으로 꺽여있는 선 ABCD 가 있습니다.
A와 B는 고정된 좌표값이 존재하며, C와 D의 좌표값은 y=x위의 임의의 점 입니다.
그러면 이때 ACDB의 최소길이는 A를 y=x에 대해서 평행이동한 A' 구했을때
A'B 의 길이와 같아집니다.
a)

이번엔 초록색 선을 지나가는 AB의 최소거리입니다.
B의 위치를 초록색 선의 길이와 방향만큼 평행이동한 B' 지점을 만듭니다.
이때 초록선이 무한히 많다면 AB'직선길이 + BB'직선거리가 최소거리가 됩니다.
물론 위의 예시에 보이듯 초록선의 갯수는 정해져있으므로
AB' 와 겹치는 초록선의 경로가 가장 짧은 거리가 될 것입니다.
이때 초록 선의 양 끝을 C,D라고하면 최소값은 AC+CD+DB가 됩니다.