-
이 과목은 본래 좌표평면이라는 이름으로 배우게 되는 내용입니다.
그러나 좌표평면 과목의 실상이 주로 두 점간의 거리를 다루므로 내용에 차이는 없습니다.
+2022-11-25 부실한 내용에 대한 설명을 새롭게 추가, 잘못된 예제 정정, 문맥정리
①P(x), P(x,y)

P(x) 는 수직선위에서 지정한 어느 한 지점의 좌표를 의미합니다.
여기에서 x는 P(3) , P(4), P(5) 등의 지정이 가능합니다.
수직선을 오른쪽 그림과 같이 위와 옆으로 두가지 기준을 지니도록 그렸을때
이것을 좌표평면 이라고 하며, (0,0)의 좌표는 원점(O) 이라는 명칭이 존재합니다.
여기에서 P(x,y) 는 x가 옆으로 이동 , y가 위로 이동을 의미하게 됩니다.
②선을 나누는 점
1)내분점

하단의 식은 왼쪽을 기준으로 합니다. 식은 내분점의 좌표 값입니다. 두 점사이에 점을 찍었을때 내분점 이라고 합니다.
내분점은 주로 1:2 같이 비를 기준으로 선을 나눌때 사용합니다.
내분점의 개념에서 1:2 와 2:1은 위치가 서로 다르기 때문에 같은 개념이 아닙니다.
위의 좌표 계산식을 반대로 해서 만약 내분점의 좌표 Q(x,y)를 기준으로 비를 구한다면
※좌표평면이 아닌 수직선이라면 Q(x)만 존재합니다.
|x(A)-x(Q)| : |x(Q)-x(B)| 혹은
|y(A)-y(Q)| : |y(Q)-y(B)| 로 구합니다.
2)내분점과 무게

두 물제가 서로 다른 거리에서 수평을 이루고
a,b는 무게 / A P B 는 각자의 위치 라고 한다면 P는 내분점입니다.
이때 선분(AP) × a = 선분(BP) × b를 만족합니다.
만약 a,b의 무게가 60, 90이라고 했을때
a:b=2:3가 양쪽에서 무게가 같기 위해선
선분(AP) : 선분(BP) = 3:2가 됩니다.
3)외분점

하단의 식은 왼쪽을 기준으로 합니다. 식은 외분점의 좌표 값입니다. 선분의 일직선상 위치에서 밖에 있는 점을 외분점 이라고 합니다.
내분점은 내분점을 기준으로 선분의 양 끝까지의 거리를 기준으로 했습니다.
이 경우 끝에 해당하는 점 중에 하나는 외분점이 되지만,
똑같이 비를 측정할때 외분점에서 본래의 선분 양끝까지의 거리를 기준으로 합니다.
그림을 보면서 비교해봅시다.
외분점을 제외한 선분의 양끝을 α , β , 외분점을 Q 라고 할때
비는 언제나 선분(αQ) : 선분(βQ) 의 비를 지니는 점Q입니다.
내분점과 마찬가지로 2:1 , 1:2의 위치가 다르며,
외분점은 더 작은 비를 지닌 방향에 위치합니다.
위의 좌표 계산식을 반대로 해서 만약 외분점의 좌표 Q(x,y)를 기준으로 비를 구한다면
|x(Q)-x(α)| : |x(Q)-x(β)| 혹은
|y(Q)-y(α)| : |y(Q)-y(β)| 가 사용됩니다.
4)중점

두점의 사이의 선분을 2등분하는 점입니다.
중점은 M으로 표기됩니다.
③유클리드 거리
1)정의

두 점 사이의 거리는 직각삼각형의 사선이라고 표현할 수 도 있습니다.
그러므로 각각의 밑변(a'-a) 과 높이(b'-b)를 구해서 피타고라스 정리로 사선의 길이를 구합니다.
이때, 거리에는 음수의 개념이 없기 때문에 제곱근의 대입으로 구해지는 음수의 해는 버립니다.
이 과정을 통해서 구하는 두점의 직선상의 거리를 유클리드 거리라고 합니다.
만약 좌표평면이 아니라 수직선상의 두 점이라면 단순히 두 값을 빼면 될 것입니다.
다만, 거리의 개념에는 음수가 존재하지 않기 때문에 절대값을 구해야 합니다.
2)응용

가끔은 유클리드 거리를 사용할 때 제곱근을 사용하지 않고 진행하는것이 더 좋을 수도 있습니다.
예를 들어서 정삼각형의 꼭지점 1개가 미지좌표 일때
미지좌표~꼭지a = 미지좌표~꼭지b 를 통해서 비교할 때 굳이 근호를 씌울 필요가 없을 것입니다.
즉, 만약에 비교 대상을 위해서 유클리드 거리를 계산한다면 선분(AB)² 상태로 활용하는 것이 좋습니다.
④삼각형
1)무게중심의 위치

무게중심은 삼각형의 점 3개의 x평균과 y평균의 위치에 존재합니다.

무게중심은 각변의 중점들로 연산을 해도 같은 결과를 얻을 수 있습니다.
2)파포스의정리

M은 선분(BC)의 중점이라고할때
선분(AB),(AC),(AM),(BM)을 모두 유클리드 공식으로 치환해서 정리된 공식입니다.
3)정삼각형의 중점

정삼각형의 중점이 수직/수평할때 꼭지점좌표는 마주보는 변의 중점의 x혹은 y좌표를 지닙니다.
보기에 당연해 보이지만 정삼각형의 양쪽 꼭지점의 좌표가 제대로 주어지지 않았을때
혹은 남은 꼭지점의 남은 좌표를 구할때 이를 떠올려야 합니다.
2.응용
A1)

선분 하나에 미지수를 주면, 이를 내분점 좌표를 구하는 식 에 대입해서 미지수를 구합니다.
가장 기초적으로 많이 볼 수 있는 유형입니다.
이를 기본 토대로 여러가지 변형을 하기 때문에 기본적으로 알아야합니다.
예를 들자면
중점m 과 외분점 Q의 거리가 1일때 Q의 좌표를 구하라고하는 등이 있습니다.
언제나 답은 같습니다. 구할수 있는 점들부터 차근차근 구해서 점들간의 거리를 구하라는 의미입니다.
A2)
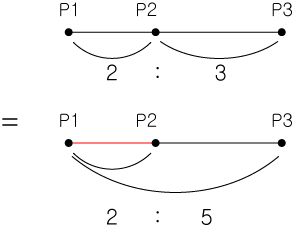
내분점 비와 외분점 비는 서로 비율을 다르게 표기하여 교환할 수 있습니다.
만약 선분2(AB)=3(BC) 라면 A,B,C간의 내분비는 3:2 , 외분비는 5:2 가 됩니다.
역으로 진행하면 외분비가 5:2 일때 내분비는 3:2가 되며 , 이때 2AB=3BC가 됩니다.
제곱에서 주의해야합니다. 내분비가 1:2라면 AB²:BC² = 1:4 이므로 4AB²=BC² 가 됩니다.
A3)

선분AP와BP의 길이가 같아지는 k값 ※예제와 다른 두번째 풀이법
A,B 두 점을 잇는 직선의 방정식을 구한후 기울기를 90도 꺽어서 A,B의 중점을 대입하면
중심이되는 축의방정식을 구할수있습니다.
축의 방정식에 0,k 를 대입하여 k=2를 구합니다.
이에 대한 개념은 다음 과정에 있습니다.
A4)

이번엔 AP+BP의 최소값입니다.
AP²+BP²을 완전제곱식으로 바꿉니다.
완전 제곱식이 (y-n)²+m 의 형태를 지닌다고 하면 최소거리는 √m 이며
y-n이 0 이되는값, 즉 최소값이 되는 y의값은 n이 됩니다.
비슷한 변형으로 x와 y 가 모두 미지수인 P(x,y)에 대한 AP+BP+CP의 최소값이 있으며,
이때는 유클리드 식을 모아서 (x-n)²+(y-m)²+k=0 으로 정리해서 x와 y값을 구할수 있습니다.
근호 미리씌워 둔 상태로 근호 내부를 완전 제곱식으로 변형하는 방법도 있습니다.
+추가 개념)

A,C가 고정값, B가 유동값이라면 B가 직선으로 그은 선분 AC 의 경로 위에 존재할때
선분(AB)+(BC)의 거리는 최소값이 될 것입니다.
A5)
y축 10지점에서 원점을향해 8의 속도로 이동중이며
원점에서도 다른하나가 6의 속도로 양의 x축 방향으로 이동할때 둘 사이 거리의 최소는?

움직이는 물체에 대해서 각각의 점은 A(0,10-8x) , B(0+6x,0)로 표현합니다.
A와 B의 유클리드 거리는 √((0-6x)²+(10-8x-0)²) 이며
이때 근호를 떼고 그냥 AB²의 상태로 진행해도 상관없습니다.
식 전개하여 완전제곱식으로 표현한뒤 최소값을 구한 뒤 근호를 씌워서 처리합니다.
A6)

점 P가 1사분면에 존재한다고하면 x>0 , y>0 일 것입니다.
점 p의 x값은 1-a 이므로 1사분면 에 존재하기 위한 a값의 범위는
1-a>0 즉 a<1 의 부등호로 변형됩니다.
A7)
주어진 비를 토대로 수직선상의 내분점, 외분점의 위치를 구할때
내분점인가 외분점인가에 따라서 양수가 되도록 7-x , x-2 로 생각해서 구할 필요가 있습니다.
만약에 식을 |x-2| : |x-7| = 4 : 1 로 두고 생각한다면
x<2 일때 x>2일때 x>7일때의 식을 전부 구해야 됩니다.