중1과정에서 배우는 기타 항목들(2)

---

①정다각형의 각도

 

 

 

n = 꼭지점의 갯수 라고할 때,

다각형의 내각의 합을 구하는 공식은 180° x (n-2) 입니다.

여기에서 만약에 도형이 정다각형이라면

내각의 합을 n 으로 나눠서 구할 수 있을 것입니다.

 

 

②다각형의 대각선

 

 

 

 

한 꼭지점에서 모든 대각선을 긋는다면 자기 자신과 양옆을 재외한 모든 점들을 이을 것입니다.

그러니까 한 꼭지점에서 그을수 있는 대각선의 양은 n-3개 라고 할 수 있을 것입니다.

 

 

 

만약에 도형이 정다면체라고 하면 a길이 = c길이 일 것입니다.

그러므로 대각선 중에 서로 다른 길이를 지니는 선의 양은

한 꼭지점의 대각선의양 / 2 를 반올림 한 값이라고 생각할 수 있습니다.

 

 

다각형이 가진 모든 대각선의 갯수를 구한다면 이렇게 생각해봅시다.

 

 

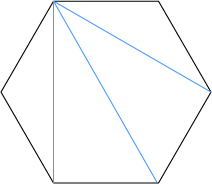
한 꼭지점의 갯수가 3개라면

 

 

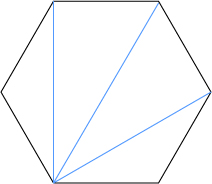
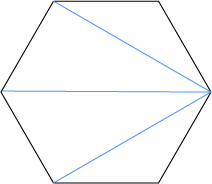
다른 꼭지점 들의 대각선의 갯수도 3개일 것입니다.

 

 

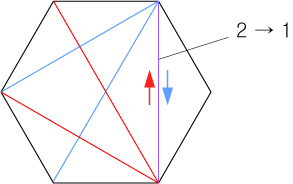
그리고 이렇게 꼭지점들의 서로의 대각선은 겹치게 될 것입니다.

그러면 겹치는 선은 2개가 아니라 1개로 계산하는 것입니다.

 

 

그렇게 된다면 모든 선은 서로 겹치게 될 것입니다.

그래서 대각선의 갯수는 한 꼭지점의 대각선 갯수 x 꼭지점의 갯수 / 2 라고 할 수 있을 것입니다.

 

 

③등변사다리꼴

 

 

 

대칭축을 기준으로 양옆이 대칭되는 사각형을 등변사다리꼴이라고 합니다.

평행돼는 두 변중에 길이가 더 긴 변의 끼인각을 밑각 이라고 합니다.

 

 

④항등식과 크기의 적용

 

 

 

넓이 , 부피등의 크기에 대한 등식에서 양쪽 모두에 미지수​가 포함되어 있다면 그 식은 항등식 입니다.