-
[미분] 삼차함수와 사차함수수학/고2 2022. 11. 14. 19:44
본 과정은 미분과의 직접적인 관계가 있는 과정이 아닙니다.
그러나 삼차함수과 사차함수를 설명하기 위해선 도함수와 극값에 대한 정보가 필요하기 때문에
정규 과목에서 미분 과정중에서 삼/사차함수에 대한 내용을 도중에 끼워놓았습니다.
이전 과정에서 배운 삼차방정식에 대한 설명(특히 근과계수의관계)는 여기에서 볼 수 있습니다.
1.개념
[삼차함수]
1.삼차함수 항의 구조 {비정규과정}
Ax³+ax²+bx+c
A=기울기 : 양수일때 증가모양을 지닙니다.
a=비틀림 : 값이 0에서 멀어질수록 극값간의 거리가 커집니다.
b=중앙기울기 : 기울기 방향은 양수일때 증가방향, 음수일때 감소방향입니다.
c=상하 평행이동 : 정확한 이동값은 완전제곱식으로 나타내야 알 수 있습니다.
2.삼차함수의 근의 범위
①실근이 3개

삼차함수의 실근이 3개 일때
극대×극소<0 가 됩니다.
②실근이 2개
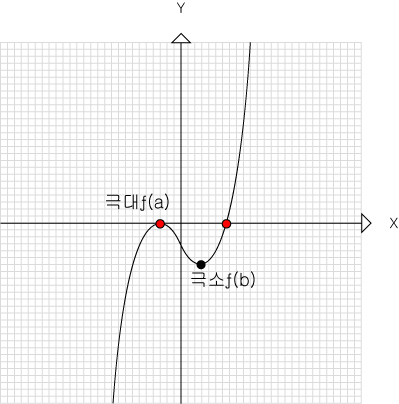
삼차함수의 실근이 2개 일때
극대값 혹은 극소값이 0 이므로
극대×극소=0 이 됩니다.
③실근이 1개

삼차함수의 실근이 1개 일때
극값이 존재하지 않거나
두 극값의 부호가 같으므로 극대×극소>0 가 됩니다.
3.삼차함수의 중근과 허근
인수분해로 근을 구할 때 모든 근을 구할 필요가 없을 수 있습니다.
예를 들어서 (t+1)(t²-2t+2)=0 이라고 한다면
t²-2t+2는 완전제곱식에서 (t-2)²+2 입니다.
(t-2)²+2 를 0으로 만들 수 있는 t의 값은 존재하지 않으므로 허근입니다.
이때 실근은 t=-1 한개가 됩니다.
이 과정의 특징에 의해서 삼차함수가 허근을 지닌다면 반드시 2개가 되며
근이 지닐 수 있는 경우의 수는 다음과 같습니다.
①실근이 3개
실근 3개를 지닙니다.
②실근이 2개
중근 1개를 지닙니다.
ex. (x-2)²(x+1)
③실근이 1개
허근 2개를 지니거나 삼중근을 지닙니다.
ex. (x-2)³
4.삼차함수와 기함수
만약 삼차함수의 중심점을 알고있다면
그 중심점 t에 대해서 ƒ(t+1)=-ƒ(t-1) 의 성질을 지닙니다.
만약 삼차 함수가 기함수라면
※본래 기함수라는 표현은 원점대칭만을 의미합니다.
비틀리면서 중심이 상향 , 하향되는 ax²
상하 평행이동을 의미하는 c 의 값이 0 이므로
그 구조는 Ax³+bx 가 됩니다.
기울기에 대한 그래프는 평행 이동과 관계 없으므로
도함수는 기함수의 여부에 상관없이
ƒ'(x)=ƒ'(-x)의 우함수가 됩니다.
[사차함수]
1.그래프 형태

사차함수는 2차함수와 마찬가지로 양수일때 위쪽을 음수일때 아래쪽을 향합니다.
(x²-1)² 같이 지수 2에 대해서 그래프로 표현하면 그 모양은 이차함수가 됩니다.
2.극값의 범위
①극값이 1개

삼중근 혹은 허근2개 일때 하나의 극값이 그림과 같이 수평해지기 때문에
극값이 1개가 됩니다.
②사중근

사중근일땐 좌우 두개의 극점이 수평해집니다.
즉, 하나있는 극점에 도착까지 기울기가 (x→0) 가 되는 수평한 구간이 넓어집니다.
이것을 극값 이라 칭할 수 있는가에 대해서는 현재의 작자로써는 모르겠습니다.
③극값이 2개
극값이 2개가 될 수 없습니다.
④극값이 3개
사중근과 ①의 경우를 제외한 나머지는 극값은 3개 지닙니다.
3.사차함수의 근의범위
그래프로 설명하자니 모양에 대한 경우의 수가 많아 아래의 정리로 통합합니다.
4.극값이 근의 크기 순으로 +a,-b,+c 혹은 -a,+b,-c 일때 근은 4개입니다.
3.양의 사차함수를 기준으로 극대가 0이면 3개입니다.
※반대로 극소가 0일땐 1,2,3개의 경우의 수가 존재합니다.
2.양의 사차함수를 기준으로 모든 극값이 음수일때 2개입니다.
1.이 외의 상황일 경우 그래프를 그려서 x축과 비교해야 합니다.
4.사차함수의 도함수 그래프
w모양의 사차함수는 감소 증가 감소 증가를 지닙니다.
극값 3개에 대해서
극소는 위→x축→아래
극대는 아래→x축→위 만 생각하면 됩니다.
2.응용
[추가지식]
양의 사차함수가 극대를 지니기 위한 조건
양의 4차함수가 극대를 지니기위해선
도함수가 서로다른 3개의 실근을 지녀야하므로
두가지의 조건을 지닙니다.
①도함수인 삼차방정식을 인수분해후 나온 2차식은 D>0 를 만족해야 합니다.
②이차식은 중근이아니며 , 이차식 밖의 다른 인수와 겹치지 않아야 합니다.
삼차식이 극대나 극소가 없기위한 조건
실근이 1개이기 위한 조건과 같습니다.
허근2개 혹은 중근 이며
만약 중근을 기준으로 잡는다면
(x+1)(중근) , (x+1)((x+1)(ax+b)) 두가지 경우의 수가 있습니다.
삼차함수의 중근 확인하기
양의 삼차함수가 중근 일때 ƒ(x)=ƒ'(x)=0
ƒ(x) = x³-3x+k 에 대해서
ƒ(x) ÷ (x-a)ⁿ = 0 (삼중근일지 , 일반 중근일지 알수 없기 때문에 지수는 n 입니다)
나머지 정리에 의해서 f'(a)=3a²-3=0 ,
도함수의 인수분해로 a를 구한뒤에 ƒ(a)로 대입하면 상수항 k가 나옵니다.
혹은 상수항이 존재하는 삼차함수에 적용해서 ƒ(a)=0이 만족하지 않으면 중근이 아닙니다.
극값을 지니기 위한 도함수 조건
f'(x)=2(x²-a)일때 a<0 일때 결과값이 0이 될수 없으므로 허근이됩니다.
그러므로 a>0 일때 함수가 극값을 지닙니다.
[풀이]
직선과 삼차식의 교점의 범위
직선과 3차방정식이 한점에서 만나려면 근이 1개일 필요가 있으므로
두 근이 허근이거나 삼중근이여야 합니다.
{-1/k+1}(x-1)=x(x-1)(kx+1)에서
(x-1)(kx²+x+1/(k+1))=0 으로 묶었을때
2차식은 완전제곱식에 의해 (x-1)²로 표현이 불가능한 일차항 계수를 지니므로
이차식은 허수입니다. (판별식 D<0)
세 실근을 지니기 위한 상수항의 범위
ƒ(x) = x³-3x²-9x+k , 두 극값의 x좌표가 -1,3
삼차함수가 세실근을 가지려면 f(-1)f(3)<0
이므로 (k+5)(k-27)<0 의 범위를 지닙니다.
사차함수의 교점이 3개가 되는 y지점
3x⁴-8x³-6x²+24x
와 y=k의 교점이 3개이므로
f(x)의 극값이 -19,13,8 일때 k=8 또는 13
-19는 최소값이라서 교점이 1개가 되어버립니다.
'수학 > 고2' 카테고리의 다른 글
[적분] 부정적분 (0) 2022.11.15 [미분 未完] 속도의 변화율 (0) 2022.11.14 [미분] 도함수 그래프와 극값 (0) 2022.11.13 [미분] 도함수의 활용과 정리 (0) 2022.11.13 [미분] 미분계수와 도함수 (0) 2022.11.12