함수와 그래프 (long)
1.함수
①함수의 정의
1)함수의 의미

함수(function)란 식을 숫자 A 로 묶어서 표현하는 방법입니다.
3 + 1 이라는 계산은 (2 + 1) + 1 이라고도 쓸 수 있습니다.
마찬가지로 f(x) = 2x + 1 이라면 2x + 1 + y 는 f(x) + y 라고도 쓸 수 있습니다.
f(x) 에서 x 는 함수가 가리키는 식의 안의 x 대신에 원하는 숫자를 대체해서 쓰라는 뜻이며
이를 통해서 f(x) = 2x + 1 일때
5라는 숫자를 f(5)로 대입해서 11로 바꾸거나 3이라는 숫자는 7으로 변형할 수 있을 것입니다.
즉 함수를 사용하는 것은 + , - , x , ÷ 말고 새로운 연산자를 만들어서 사용한다 라고도 생각할 수도 있습니다.
2)함수의 종류

- 상수함수 : x에 어떤값을 넣어도 항상 같은 값이 결과로 나오는 함수입니다.
- 분수함수 : 함수 안의 식에서 x가 분모로 사용되는 함수 입니다.
- 일차함수 : x 의 차수가 1인 함수입니다. 혹은 x에 대한 일차식 이라고도 합니다.
3)함수의 표기

여러개의 함수를 사용할 때는 f(x) , g(x) , h(x) 순으로 나열해서 쓸 수 있습니다.
②함수의 특징
1)방정식을 함수로

y = x + 1 일때 x = 3 이면 y = 4 일것입니다.
f(x) = x + 1 일때 f(3) 이면 f(3) = 4 일것입니다.
즉, y = nx + m 과 같이 y에 대한 식의 정리가 끝나있다면
이것을 f(x) = nx + m 이라고 바꿔서 적을 수도 있을 것입니다.
그래프에서 만약 식이 f(x) = ax + b 같이 쓰여있다면
y = ax + b 라고 해석해서 보라는 뜻이기도 합니다.
2)함수 끼리의 연산

f(x) + f(x) 같이 미지수인 두 함수를 연산해야할 때는 함수 안의 식의 내용을 풀어서 작성합니다.
만약에 그 식이 등식이였다면 등식을 만족하는 x의 값을 구할 수 있습니다.
3)함수식의 추정
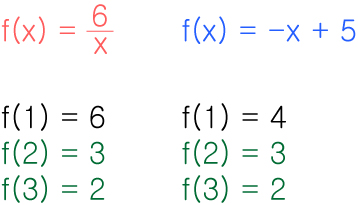
함수식을 제대로 추정하기 위해선 최소 3개의 결과 값이 필요합니다.
덧셈과 뺄셈을 사용하면서 다른 식임에도 부분적으로 같은 결과가 겹칠 수 있기 때문입니다.
즉 f(2) = 4 라고해서 f(x) = 2x 라고 추측해선 안됩니다.
4)함수식에 식을 대입

f(x) 에서 x 는 식안에있는 모든 x 를 괄호안의 숫자로 대체하라는 뜻입니다.
즉, 외부에서 x = 1 이라는 해가 구해졌어도 함수를 f(x+2) 같이 사용한다면
f(x) = 3x - 6의 식에서 모든 x들을 x+2로 바꿔 f(x+2) =3(x+2) - 6 로 해석해야합니다.

f(x-1) = 3x - 6 과같이 괄호안의 식과 함수식의 x 정보가 일치하지 않을 수도 있습니다.
이것이 뜻하는 바는 f(x-1) = ?(x-1) + ? 의 함수식이 따로 존재한다는 것이고
?(x-1) + ? 라는 식의 결과 값이 3x - 6 의 결과 값과 같아서 등식으로 서로 이어져 있는 것입니다.
그래서 이럴 때는 x를 x-1로 대체하라는 뜻이 아니므로 직접 x의 해를 대입하는 것이 맞습니다.
2.그래프
①함수를 그래프로 그리기
1)그래프 그리기

y = x 라면
y 가 1일때 x 도 1일 것입니다.
그러면 (1,1) 인 지점에 이렇게 점을 찍을 수 있습니다.

마찬가지로 y 가 2 일때 x 는 2일 것이고 (3,3) , (4,4) , (5,5) ... 의 여러 점들이 찍힐 것입니다.

한편 y가 0.1일때 x 도 0.1 일 것이고 (0.4,0.4) , (0.63,0.63) ... 이렇게 모든 지점들에 점을 찍게 된다면
이 모든 지점들이 모여서 선으로 보일 것입니다.
2)그래프의 기울기

y = 1/2x 에서 y에 1을 대입해봅시다. 1 = 1/2x 이므로 정리하면 x = 2 입니다.
그러므로 y 가 1 일때 x 는 2 일 것입니다.
x 의 기울기가 0.5 라고 y 1칸당 x 0.5칸으로 착각하기 쉬우니 주의가 필요합니다.

y=2x 그래프에선 y가 1일때 x는 0.5가 될 것입니다.
x의 계수에 따라서 그래프의 기울기가 달라지므로
x의 계수는 기울기를 의미한다고 할 수 있습니다.
3)그래프의 이동
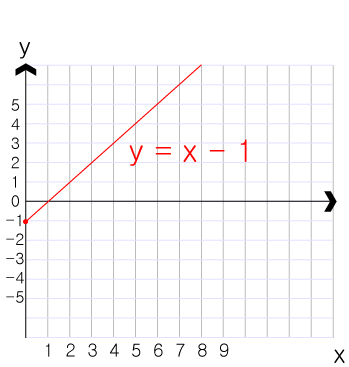
y = x - 1 에서 x = 0 이라고 해봅시다.
그러면 이때 y = -1 이 될 것입니다.
여기에서 x = 1 일때 y = 0 일것이고 (2,1) , (3,2) , (4,2) ... 의 지점들을 지날 것입니다.
이를 눈으로 보았을때 결국 y = x 그래프에서 -1을 하면 그래프를 한칸 아래로 이동한 결과로 보입니다.
즉, 그래프에서 상수는 y축으로 그래프를 평행이동하는 효과가 있다고 할수 있습니다.
4)그래프와 음수

식에서 x 값이 음수가 되면 y축을 기준으로 선이 반전되는 효과가 있습니다.
②함수 그래프의 특징
1)절편

그래프나 x축이나 y축을 지나칠때 만나는 점을 절편 이라고 합니다.
이렇게 축과 선이 겹쳤을때를 x축/y축위에 만나다 라고 표현합니다.
위의 그래프에서 x절편은 (1 , 0) 이고 y절편은 (0 , -1) 입니다.
반대로 말해서 계산한 좌표 값에 x 값이나 y값에 0이 나오면 그 값이 x나 y의절편이라는 뜻도 됩니다.

x가 0일때 상수만 남으므로 함수에서 상수는 y 절편과 항상 일치합니다.
한편 x의 절편은 y가 0일때를 뜻하므로 y에 0을 대입해서 0 = x -1 의 등식으로 구할 수 있습니다.
위의 식에서 x의 절편은 1 일 것입니다.
2)축에 평행한 그래프

위의 그래프 y축에 평행한 모습입니다.
y값이 몇으로 변하건 상관없이 x의 값은 항상 6일 것입니다.
즉, 이 선의 모양에서 y는 상관이 없습니다.
그래서 이럴 때는 y 를 빼고 x = 6 그래프 라고 합니다.

반대로 식이 y = 1 같은 상수함수라면 이 그래프는 x축에 평행한 그래프가 됩니다.
y = 1 의 그래프는 y값에 상관없이 x가 ∞ 인점과 -∞ 인점을 지날것이므로 두 점을 이으면 가로가 될 것입니다.
그러므로 x = 1 그래프도 y 를 -∞ ~ ∞ 점 까지 이으면 세로가 될 것입니다.
3.함수의 응용
①함수식 안의 함수

함수식 안에 함수가 들어가고 같은 x 를 사용하고 있을땐
x 값을 공유하여 식 안의 함수먼저 순차적으로 풀어 나갑니다.

반면에 함수안의 미지수가 밖의 함수와 서로 다를경우엔 x 값 외에 y값을 같이 받아야만 계산할 수 있습니다.
②함수식안의 미지수

함수의 결과 값이나 x의 해와 비교해보면 함수안의 미지수를 추측할 수 있습니다.
4.그래프의 응용
①평행선의 특징

만약 y축에 평행한 그래프가 있다면 순서쌍 (x,y) 에서 x의 값은 y값에 상관없이 항상 같을것입니다.
즉, 위의 예시에서 3a = -2a + 10 이며 a = 5 라는 것을 알수 있습니다.
이 때, 좌표에 a 값을 대입해서 구하는 x의 값은 15가 될 것입니다.

y = ax + 3 과 y = 2x - 4 가 서로 평행하다고 하면
두 함수의 기울기는 같을 것입니다.
즉 ax = 2x가 될 것입니다.
②두 좌표로 함수식 구하기

y = -1/2x 에 대해서 생각해봅시다. y = 1 일때 x = -2 일것입니다.
다른말로 표현하자면 y 축으로 1 움직일때 x축으로 -2 만큼 움직인다는 것입니다.
큰 톱니바퀴가 2바퀴 회전할때 작은 바퀴가 3회전했다면 작은 바퀴는 큰바퀴의 3/2배 회전 했을 것입니다.
마찬가지로 x 가 -2 움직였을때 y 가 1 움직였으므로
x는 y 의 1/-2배 움직인다고 할수 있으며 이것은 기울기를 의미합니다.
그러므로 x 와 y 축으로 좌표가 얼만큼 움직였는지 알수있다면 그래프의 기울기를 구할수 있을 것입니다.
두 좌표 (2, -2) 와 (6 , -4)를 비교해보면, 두 좌표의 x 값이 4 만큼 차이나고 y 값은 -2만큼 차이납니다.
즉 , x 는 y 의 -2/4 배 이므로 두 좌표를 비교해본 결과, 이 그래프의 기울기는 -1/2 라는것을 알 수 있습니다.
이렇게 구한 기울기를 좌표 (2, -2)에 적용해서 (0 , ?) 로 만들어보면
x 가 -2움직일때 (2 → 0) y 는 1 움직일 것이므로 (-2 → -1)
이렇게 만들어지는 좌표 (0, -1)는 y 의 절편입니다.
혹은 방정식을 y=ax+b 라는 미지수로 표현하고
위의 계산으로 기울기를 구해서 y=-½x+b에 y=-2 , x=2를 대입해서 b값을 구할 수 있습니다.
(2,-2) , (6 -4) 의 좌표를 지니는 함수는 기울기 -1/2 상수항이 -1이므로 y = -1/2x -1 함수라는것을 알 수 있습니다.
이 계산은 어디까지나 함수가 일차함수라는 전제가 있어야만 적용 가능합니다.
응용2) 3개의 좌표로 좌표 안의 미지수 구하기
(2,-2) , (6,-4) , (a,2) 3개 의 좌표가 주어진다면 그 중 2개를 이용해서 함수를 구할 수 있을 것입니다.
이 함수는 y = -1/2x - 1 이므로 여기에 남은 좌표 (a,2) 의 2를 대입해보면
2 = -1/2x -1 , 3 = -1/2x , x = -6 이므로 ∴ a = -6 이란 것을 알 수 있습니다.
③그래프 도형
1)그래프도형의 넓이와 교점 구하기

교점의 좌표는 두 개의 함수 그래프의 연립방정식을 통해서 구할 수 있습니다.

계산해보면 교점은 (1,4) 이므로 x축(0)을 기준으로 삼각형의 높이는 4 입니다.

x축을 기준으로 밑변의 양 끝은 각 함수 그래프들의 x절편 이므로 y에 0을 대입해서 구할 수 있습니다.
y = x + 3 → 0 = x + 3 → x = -3
y = -2x + 6 → 0 = -2x + 6 → x = 3
이때 -3 과 3의 거리는 |6| 이므로 밑변의 길이는 6입니다.
그러므로 삼각형의 넓이 밑변(6) x 높이(4) ÷ 2 = 12 입니다.
2)그래프 함수가 삼각형을 이루지 못 하는 조건
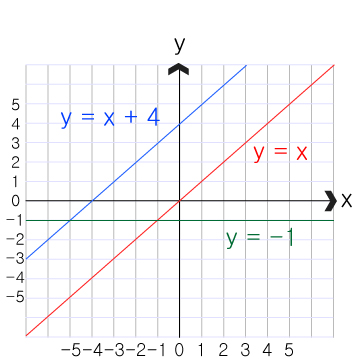
삼각형을 이루는 변 중에서 두 선이 평행하다면 삼각형이 이루어지지 않습니다.

3개의 선이 같은 교점을 지닐때도 삼각형은 이루어지지 않습니다.
ex.기타사항
1. 1m 단위로 쓰는 그래프에서 50cm 는 0.5 혹은 1/2라고 표기해야함을 주의합시다.
혹은 1시간 단위 의 그래프일때 30분은 0.5 혹은 1/2일 것입니다.
2. 항등식의 특징 을 응용해서 기울기와 상수를 구하는 경우가 간혹 있습니다.
만약에 ax + 3 = 3x + b 같이 양쪽의 항이 쌍을 이루며 동류항이면 의심해봅시다.
3.y = x + 1 은 f(x) = x + 1 로도 표현할 수 있다고 했습니다.
그래서 (1, 3) 라는 좌표가 있을때 이것을 (1 , f(1)) 라고도 표현할 수 있습니다.
식을 알고있다면 x 와 y 값중에 하나만 있어도 다른 한쪽 값을 추정하는 것이 가능하기 때문에
데이터의 보관을 x 하나로 간소화 하기위해서 사용됩니다.
4.1시간동안 2km이동 , 1°C 오를때마다 물의 증발량이 10mL 상승 등 그래프로 표현 가능한 문제들은
대부분 f(x) = ?x 식으로 변경할 수 있습니다.
예를들어
1시간 동안 2km 이동이므로 식으로 표현하면
시간을 y로 보면 f(x) = 1/2x (y가 1칸이동할때 x는 2칸 이동하므로)
이동거리를 y로보면 f(x) = 2x 로 표현할 수 있을 것입니다.