원의 구성 과 부채꼴의 특성
+2022-11-18 링크 위치 수정 , 소량의 문맥 수정
1.원주율과 반지름의 표기
①파이
π
원주율을 사용한 계산에서 3.14로 뒷자리를 버리고 쓰는것이 정확한 계산이라고 할 수 없습니다.
그래서 중학교 과정부터 3.14159265... 을 π(파이) 라는 기호로 씁니다.
②반지름 r
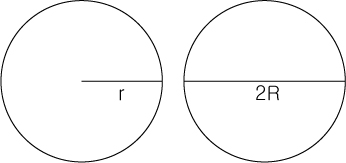
원에서 반지름을 미지수로 쓸 때는 주로 r(radius 반지름) 이라는 기호를 사용합니다.
이때, 지름은 2r 혹은 2R 로 표기됩니다.
2.원의 구성
①원의 구성

- 임의 정한 곡선의 범위를 호 라고 합니다.
- 원의 내부를 지나가는 선분을 현 이라고 합니다.
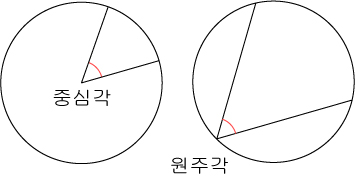
- 원의 중심을 지나는 두 현의 끼인각을 중심각 이라고 합니다.
- 두 현이 원의 변에서 만나서 끼인각을 이루면 원주각 이라고 합니다.
②원주각의 특징
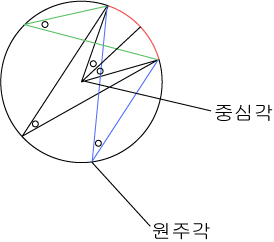
지니있는 호가 같다면 원주각은 방향에 상관없이 항상 같은 크기를 지닙니다.
최하단 (1)번 증명에서 이유를 설명합니다.
원주각과 중심각이 지닌 호가 같을 때 원주각은 중심각의 1/2배가 됩니다.
최하단 (2)번 증명에서 이유를 설명합니다.
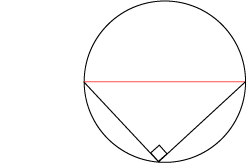
만약에 지닌 호가 원의 절반 지점의 크기라면 원주각의 크기는 90° 가 됩니다.
3.부채꼴과 활꼴
①부채꼴과 활꼴의 정의

원의 중심을 기준으로 현으로 원을 자른 모양을 부채꼴 이라고 합니다.그 중에서 반원의 모양을 하고 있는 부채꼴은 활꼴 이라고도 합니다.
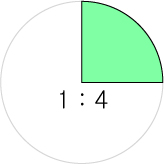
부채꼴이 원의 1 : 4 의 비율을 가질 때,
부채꼴의 넓이는 원의 1/4 크기를 지닐 것입니다.
또한 부채꼴의 호의 길이는 원의 둘레의 길이의 1/4 크기를 지닐 것입니다.
이것을 정리하면, 위의 원에 대한 식을 정리하면
부채꼴의 둘레는는 2R(지름) × π(원주율) × 1/4(비율) + 2r(두 반지름) 이며
부채꼴의 넓이는 R²(반지름제곱) x π x 1/4(비율) 입니다.
②부채꼴의 특징
1)부채꼴과 비율
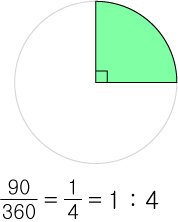
원의 한바퀴를 돌기위해서 필요한 각도가 360° 가 필요합니다.
부채꼴이 90° 라고 할때, 부채꼴은 원의 360° 중에 90° 를 차지하고 있다고 생각할 수 있습니다.
이것을 비율로 정리하면 1 : 4 입니다.
2)부채꼴의 각도
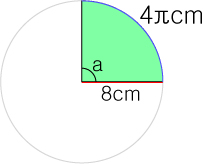
만약에 반지름(r) 과 호의 길이를 알고 있다면 부채꼴의 중심각의 크기를 알 수 있습니다.
원주 = 지름 x π 이므로 예시의 원의 원주(원의둘레)는 16π 라는 것을 알 수 있습니다.
이때 부채꼴의 호의 길이는 4π 였으므로, 이 부채꼴의 비율은 1 : 4 입니다.
이때 360 x 1/4 = 90 이므로 a 의 각도는 90도 라고 할 수 있습니다.
3)부채꼴의 부분 넓이

호의 임의 범위를 기준으로 평행선을 그어서 위와 같은 도형 그렸을 때
위의 두 도형의 넓이는 같습니다.
최하단 (3)번 증명에서 이유를 설명합니다.
4)2개의 호로 만들어 지는 넓이
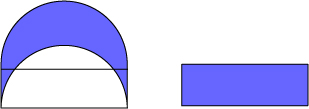
직사각형의 평행한 두 변을 호로 만들었을때
이 직사각형과 휘어진 도형의 넓이는 같습니다.
(4)번 증명에서 이유를 설명합니다.
5)2개의 부채꼴의 겹침각

같은 반지름의 부채꼴을 겹쳤을 때 그 각도는 30° 가 됩니다.
Ex. 증명
①같은 호에서 중심각이 원주각의 2배인 이유
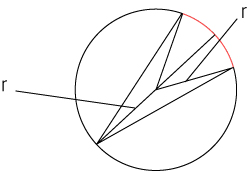
같은 방향을 지니는 원주각과 중심각을 같이 그린뒤에 중심으로 선을 그었습니다.
이때, 중심각의 양쪽 현과 관통하는 선의 반은 원의 반지름이라고 할 수 있을 것입니다.

여기에서 발생하는 두개의 삼각형은 두변의 길이가 같으므로 이등변삼각형입니다.
이등변 삼각형의 두 내각은 똑같은 각도 ∠x 일 것이며
삼각형에서 남은 한 내각을 중심으로 하는 외각은 ∠x + ∠x 일 것입니다.
이는 반대편 삼각형도 마찬가지일 것이므로
결국 중심각은 원주각의 2배라고 할 수 있습니다.
②같은 호에서 모든 원주각의 크기가 같은 이유

중심각을 ∠a 라고하고 원주각을 ∠b 라고 해봅시다.
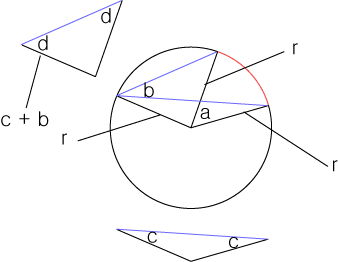
a와 b 의 꼭지점을 잇는 선분을 그었을 때,
중심점에서 부터 원의 변으로 향하는 모든 선은 반지름이라고 할 수 있을 것입니다.
반지름 r 은 모두 길이가 같을 것이므로 이에 따라서 두변의 길이가 같은 이등변 삼각형이 2개 생깁니다.
이등변삼각형들의 양쪽 동일한 내각을 ∠c , ∠d 로 취급했을때,
∠d = ∠c + ∠b 인것을 눈으로 확인할 수 있습니다.
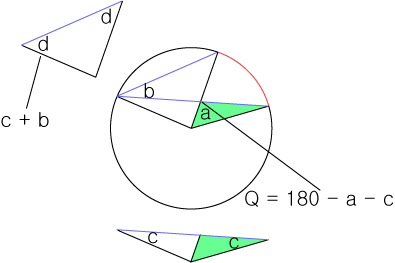
모든 삼각형의 내각은 180도 이므로 칠한 영역에서 교차점을 Q 라고 할때
∠Q = 180 - a - c 라고 할수 있을 것입니다.
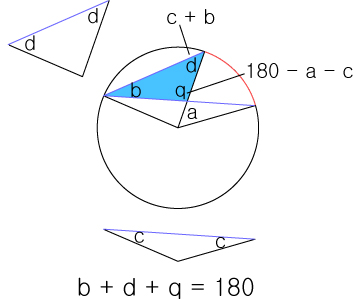
그리고 ∠Q 에 직접 대응하는 동위각 ∠q 는 ∠Q 와 같을 것이며,
이때, b , d , q 는 삼각형을 이루기 때문에 합이 180도 일것입니다.

여기에서 b 하고 q 를 앞서 구한 식으로 대입해서 정리해보면b = 1/2a 즉, a = 2b 라는 결론에 다다르게 됩니다.
즉 호의 길이가 같을때, 원주각을 다른 방향의 현으로 그려도 각도는 같은 것을 알수 있습니다.
③부채꼴 내부의 현이 중심을 향할때와 평행할때 넓이가 같은 이유
※내용물을 이해하기 위해선 합동에 대해서 알고 있어야 합니다.
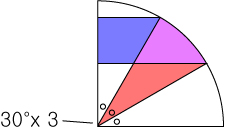
편의를 위해서 3등분된 호를 기준으로 예시의 두개의 도형을 곂쳐놨습니다.

우선 위의 두 각은 90°로 같습니다.
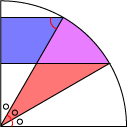
두선이 평행하므로 이 두개의 엇각은 서로 같습니다.

이번 예제에서는 호를 정확히 3등분 했기 때문에,
위의 60도를 기준으로 둘은 같은 크기라는 것을 알 수 있습니다.

그리고 중심점을 향하는 두 선은 반지름에 해당하므로 같은 길이입니다.

하므로 빨간선으로 구분되는 삼각형과 파란선으로 구분되는 두 삼각형은
ASA합동입니다.

즉, 두 삼각형의 넓이는 같을 것이며, 이를 토대로 정리해본다면
자주 + 파랑 = 빨강 + 자주 라는 것을 알수 있습니다.
④두개의 호로 직사각형을 휘어도 넓이는 같은 이유
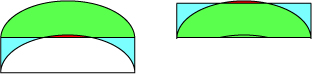
휘어진 사각형을 원본 사각형의 형태로 자른뒤에 위로 곂쳐보면 넓이가 같음을 알 수 있습니다.