그래프와 비례
그래프는 예측의 기본입니다.
만약 데이터를 다루는 직업에서 가장 기초적으로 많이 쓰입니다.
1.그래프

좌표 평면을 이용하여 두개의 물질의 관계를 눈으로 보여주는 그림을 그래프 라고 합니다.
여기에서 x 와 y 이에는 어떤 것이든 들어갈 수 있습니다.
예를 들자면 시간 당 매출 , 온도 당 외출인원 , 무게 당 들수있는 사람의 수 등이 있습니다.
이때, 시간, 온도, 무게 처럼 정확하게 나누어지지 않는 연속형 데이터가 주로 x 축이 됩니다.

그래프의 선이 오르는 모양이면 이것을 x(물가) 와 y(년) 는 정비례 한다고 합니다.

그래프의 선이 내려가는 모양이면 이것을 x(출산율) 와 y(년) 은 반비례 한다고 합니다.
2.그래프 응용

한 거북이가 목적지를 향해 가던중에 두고온 물건이 생각났다고 가정해봅시다.

그러면 거북이는 대중교통을 기다리다가 잠시후 다시 돌아갈 것입니다.

그리고 다시 출발 해서 도착했다고 했을 때, 그래프는 이런 모양 일 것입니다.

0에서 1시간 까지의 거리를 분석해 본다면 거북이는 1시간에 0.7km 를 이동했다고 할수 있습니다.
여기에서 0.7km 는 700m 로 바꿀수 있고 1시간은 60분으로 바꿀 수 있습니다.
그렇다면, 거북이는 6분마다 70m 를 이동 한다는 것이고
1분마다 약 11.6m 씩 이동한다고 가정했을때,
10분뒤에 거북이는 약 700m + 11.6 x 10 의 지점에 있다고 예측할 수 있습니다.
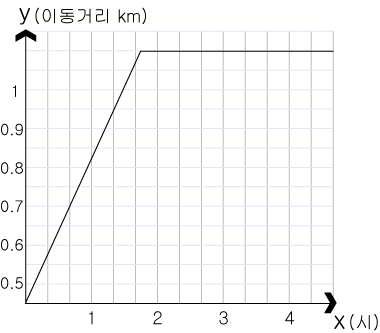
반면 저 그래프를 토끼의 그래프와 비교해보자면
토끼는 목적지 까지 의 거리가 더 멀다는 것을 파악 할수 있습니다.
하지만 그래프의 정지 구간으로 봐서, 토끼는 거북이보다 일찍 도착했습니다.
3.그래프의 식 표현

한편 거북이의 1시간 구간을 확대하면 이런 그래프를 얻을 수 있습니다.
1분마다 약 11.6m 씩 이동하는 그래프이므로

즉 위의 그래프는 y = 58/5 x 그래프 라고 할 수 있습니다.
만약에 x 에 30의 값을 대입 한다면,
30 x 58/5 = y
6 x 58 = y
∴ y = 348
즉 , 30 분이 지났을 때, 거북이는 0.346km 를 이동했다고 할수 있습니다.
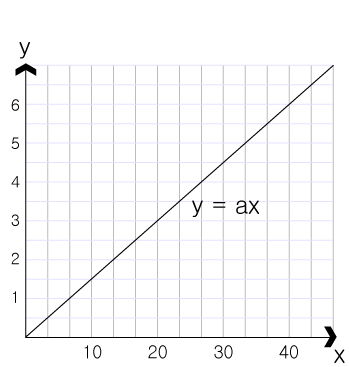
이렇게 x 가 분자 계산되어 위치한다면 그 그래프는 정비례한 모습을 보입니다.

만약 x 가 분모로 가게 된다면 그 그래프는 반비례한 모습을 보입니다.
