[수열] 등비수열
1.개념
[등비수열]
1.정의
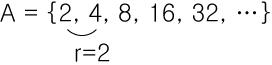
이웃한 항 간에 서로의 비를 a₁ : a₂ 라고할때
어느 지점에서도 그 비가 항상 일정한 수열을 등비수열이라고 합니다.
항의비를 1:r로 두었을때 r(rate)을 공비 라고 합니다.
2.일반항

첫째 항이 2 , 공비 r이 2 라면 a₁=2×1(2⁰) , a₂=2×2 가 됩니다.
3.등비중항
a₁과 a₃ 사이의 등비 중항이 a₂ 라고 한다면 그 계산식은 √ab (a>0, b>0) 가 됩니다.
이 식은 기하 평균과 정확히 일치하지만,
기하평균의 본래의 사용법이 등비 중항과 조금 다른 개념입니다.
4.특성
①
변수가 지수에 존재하기 때문에 그래프로 표현하면 지수함수가 됩니다.
단, n이 자연수이기 때문에 정수마다의 점선의 형태를 지니게 됩니다.
②
두 등비수열의 곱을 {An}×{Bn}={Cn} 이라고 할때 {Cn}은 등비수열이 됩니다.
2.응용
※보통 수열에 쓰는 말줄임 표시는 아래쪽이 아닌 중앙점 을 사용합니다.
[추가 지식]
1.A≥G≥H 는 등비수열
a+b/2 와 2ab/a+b의 등비중항은 √ab 이므로 평균들 간에 등비수열이 성립합니다.
그렇다면 절대부등식 A≥G 에 대해서 G≥H 도 반드시 성립할 것입니다.
2.음수에서 시작하는 항에 따른 일반항의 조정
A = {√2-1,1,√2+1,…} 에서 첫째항부터 k항까지 음수부터 시작할때
일반항을 (√2+1)ⁿ⁻² 와 같이 조정할 수 있습니다. (n-1-(음의항갯수k))
3.모든 값이 같은 수열
A = {1,1,1,…} 일때 수열 A는 등차수열이자 등비 수열 입니다.
d=0 , r=1이 됩니다.
[기본]
※입력상의 한계로 작은 n을 일반 n으로 작성하였습니다.
①
an = 2²ⁿ⁺⁴
= 4ⁿ⁺²
= 4³*4ⁿ⁻¹
∴ r = 4 , a₁=4³
②
a₂=ar=6 , a₅ =ar⁴=-48
→ ar⁴/ar=r³=-8
∴ r=-2
③
a₁+a₂+a₃=14 , a₄+a₅+a₆=112
→ a+ar²+ar³=14 , r³(a+ar²+ar³)=112
∴ r³=112/14=8
다만, 이경우엔 r³를 기준으로 묶는것 외에도 a₁r , a₁ 등을 기준으로 묶을 수도 있습니다.
[테크닉]
①
r+r²+r³ = 0 , r≠0
→ r(1+r+r²)=0
∴ (1+r+r²)=0
[풀이]
1.공비가 같은 두 수열의 합의 일반항
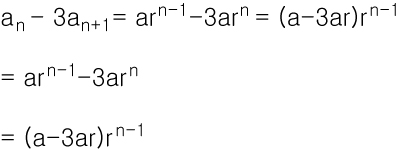
예시에서는 자기자신의 합이 사용되었습니다.
r에대하여 정리된 준식의 첫째항은 a-3ar가 됩니다.
2.등차수열의 일부가 등비일때
등차수열의 항들중에 a₂,a₄,a₉ 가 등비일때 a+d,a+3d,a+8d로 나타낸다면
등차중항에의해 (a+3d)²=(a+d)(a+8d) → d=3a
항에서 d를 a로 바꿔서 a₄/a₂ = 10a/4a = r = 5/2
즉 , 첫째항은 4a , 공비는 5/2 입니다.
여기에서 a란 등차수열의 첫째항 값입니다.
위의 풀이에서 주목해야 하는 특성은 등차수열에서 추출하는 공비는
공차의 값에 상관없이 추출한 항의 순서에 의해서만 결정 된다는 점입니다.
[심화]
※입력상의 한계로 작은 n을 일반 n으로 작성하였습니다.
작성된 내용은 틀을 깨고 등비수열의 일반항에 대한 새로운 접근방법을 소개합니다.
이후의 수학을 배우는데 필요한 이론도 아니고,
이 지식이 실용적으로 쓸수 있는가에 대해서는 의문이기에
궁금한 사람만 보라는 의미로 접어둡니다.
an =arⁿ⁻¹ 에서 a₁=2 , r=3 이라고 가정해봅시다.
x=3 라고 한다면 a=x-1 , r=x 가 되겠죠
그러면 , xⁿ⁻¹(x-1) 라고 표현하고 이걸 ƒ(x) 라는 함수로 표현할 수 있습니다.
이때 이 ƒ(x)는 공비와 첫째항의 차이가 1인 모든 등비수열들을 의미합니다.
ƒ(x)를 x-3으로 나누는 것은 ƒ(3) 하고 동일하죠?
그리고 ƒ(3)의 결과값으로 나오는 값은 나머지 입니다.
x=3일때 ƒ(x)는 위의 a₁=2 , r=3의 일반항이 됩니다.
an =arⁿ⁻¹ 라면 , arⁿ⁻¹=an 이겠죠?
그래서 ƒ(3)=an 즉, ƒ(x)에 x-3을 나눈 나머지는 등비수열의 항이 됩니다.
원하는 순서의 항을 구하겠다면, 자연수 n의 값은 미리 정해두고 계산해야 될 겁니다.