2.이차함수의 그래프 응용
https://mytory.tistory.com/118
이차함수의 그래프
https://mytory.tistory.com/101 함수와 그래프 (long) 1.함수 ①함수의 정의 1)함수의 의미 함수(function)란 식을 숫자 A 로 묶어서 표현하는 방법입니다. 3 + 1 이라는 계산은 (2 + 1) + 1 이라고도 쓸 수 있습..
mytory.tistory.com
이전 글에서 이어지는 내용입니다.
①그래프 평행이동하기

먼저 그래프를 평행이동에 알맞게 변형합니다.
x축으로 3 이동할 때 이차항에 -3을 대입해줍니다.
y축으로 3 이동할 때 상수항에 3을 대입해줍니다.
②좌표값으로 미지수 구하기

좌표는 하나의 점을 뜻하기 때문에 이차함수의 좌표는 어느 한쪽 날개의 한 지점을 뜻합니다.
즉 좌표는 (-x,x) 를 뜻하는 것이 아니라 (x,y)를 뜻합니다.
③절편으로 이차함수 추측하기
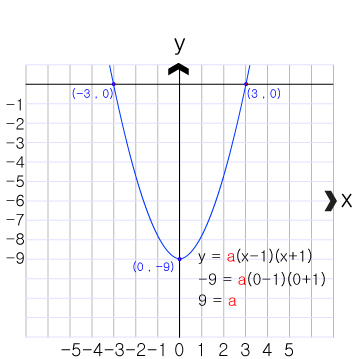
x 절편의 두 좌표를 가지고있다면 0 = a(x+3)(x-3) 이라고 표현할수 있습니다.
함수식의 상수항은 y = a(x+b)² + c 일때를 기준으로 하므로 상수항이 맞지 않는게 정상입니다.
y 절편 (0,-9)을 지나간다고 했을때 이를 식에 대입해서
-9 = a(0+3)(0-3) 이므로 기울기 a = 1 입니다.
즉 이 그래프는 (x+3)(x-3) 그래프이므로 y = x² - 9 그래프 라고 할 수 있습니다.
④좌표를 대입해서 평행이동한 함수 추측하기

Y 축으로 평행이동된 함수는 (x+1)²-18+m 으로 표현할 수 있습니다.
만약 평행이동한 함수가 좌표 (1 , 3) 을 지나간다면
3 = (1+1)²-18+m 이므로 m의 좌표를 구할수 있을 것입니다.
y = x²+2x+2+m 처럼 정리되지 않은 식에 m을 대입하지 않도록 주의해야합니다.
⑤y축으로 평행이동한 선상의 좌표 거리 비교

y축으로 평행이동을 한 그래프의 거리가 x축 위에서 원본의 1/3 이며
원본함수의 x 절편이 (x1 = 4 , x2 = -2) 주어졌을때
4과 -2은 1(4 - (4-(-2))/2)을 기준으로 대칭하고 있으므로
1을 기준으로 양쪽값의 거리를 1/3 하면 이동한 그래프의 x 절편을 구할수 있을 것입니다.
기준점을 0에 맞춰서 평행이동하고 (3(4-1) , -3(-3-1))
(3,-3)을 1/3해서 다시 기준점을 1로 되돌리면 (2(1+1),0(-1+1))
평행이동한 그래프의 x 절편이 (x1 = 2, x2 = 0) 이라는 것을 알수 있습니다.
⑥이차함수간의 넓이

원리는 평행한 두 호의 넓이 와 같습니다.
사선간의 거리가 아니라 상하간의 거리이기 때문에 양변의 길이는 같아집니다.