도형과 비율(short)
①넓이의 비

두 도형이 닮은 도형 이라면 닮음의 비를 사용합니다.
만약에 두 도형이 닮은 도형이 아니라면,
넓이를 기준으로 하는 넓이의 비를 사용할 수 있습니다.

넓이의 비는 닮음의 비의 제곱을 항상 만족합니다.
②삼각형의 변과 넓이의 관계

높이가 같고 밑변의 길이만 서로 10% 차이나는 두 삼각형이 있다고 해봅시다.
삼각형의 넓이를 S 라고할때, 이 둘의 넓이의 비는
S : S + 10% 가 될 것입니다.

밑변이 아니더라도 어느 한 변의 길이가 10% 늘어나면 넓이도 10% 상승합니다.
③평행선과 도형의 비

삼각형을 변 하나에 평행하게 자른다면 내부의 삼각형들은 모두 닮은 도형입니다.

만약에 평행선들 간의 거리가 일정하다면 변이 일정한 길이로 나뉘어질 것입니다.
내부의 삼각형들은 닮은 도형들 이므로 변의 길이에 따라서 삼각형들의 닮음의 비를 구할 수 있습니다.
또한 닮음의 비를 응용해서 변의 길이의 비를 추측할 수 있습니다.

또한 이를 통해서 두개의 평행선의 길이를 통해서 내부의 평행선의 길이를 추측할수 있으며

닮음의 비를 생각한다면 길이의 차이를 총해서 선의 길이의 비를 추측할 수도 있을 것입니다.
④미지수와 비

직각삼각형의 넓이가 16cm² 이며 밑변과 높이 길이는 1 : 2 를 만족합니다. 여기에서 높이를 구한다면,
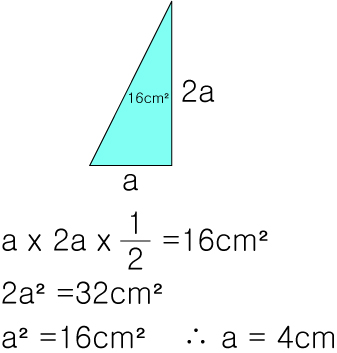
모르는 숫자를 미지수 a 라고 가정했을때 밑변과 높이의 길이는 a : 2a로 표기할 수 있습니다.
이렇게 만들어진 미지수를 넓이의 식에 대입해서 등식을 만든다면 a의 값을 통해 높이를 구할 수 있습니다.
⑤그래프와 비

그래프에서 선의 기울기란 y로 몇번 x로 몇번씩 이동하는가라고 판단할수 있습니다.
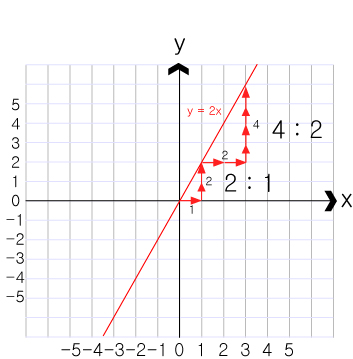
떨어진 거리에서도 y 와 x 의 비는 언제나 유지될 것입니다. 그러므로 이것을 y : x 로 표기할 수 있을 것입니다.

y : x 의 비율을 통해서 미지수의 거리를 추측할 수 있습니다.
