평균과 중앙값
평균은 특히 매우 중요한 개념입니다.
이번엔 평균이 무엇인지 살펴보고 비슷한 개념인 중앙값 과의 차이를 알아봅시다.
1.평균의 개념
평균이란 여러가지 숫자들이 있을 때 그 숫자들의 중심이 되는 지점의 숫자를 뜻합니다.
예를 들자면,

숫자 1 과 3이 있을 때 그 중심이 되는 값은 2 라고 할 수 있습니다.
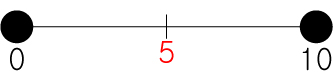
숫자 0과 10의 중심이 돼는 값은 0,1234 5 6789,10 라고 본다면 5가 될 것입니다.

이런경우 1,2345 5.5 6789,10 로 볼수 있으므로 평균은 5.5가 될 것입니다.
위의 3가지의 예시를 통해서 중심이 되는 값이란 것이 무엇인지 제대로 파악해봅시다.
2.평균의 특징

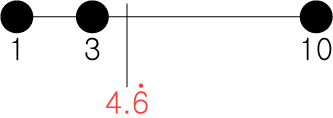
만약에 사용되는 숫자가 3개 라면 어떨까요? 이럴 때에도 평균값은 5.5 일까요?

이럴 때는 숫자를 두개씩 읽어봅시다. 1과7의 평균은 4 , 7과10의 평균은 8.5가 일 것입니다.

그리고 4 와 8.5 의 평균은 6.25 입니다. 즉, 1/7/10 의 평균은 5.5 보다 높은 6.25 라고 할 수 있겠습니다.
즉, 이를 통해서 알 수 있는 사실은 높은 숫자가 많을수록 평균은 더 높아 질 것이라는 것 입니다.
반대로 작은 숫자가 많아질수록 평균은 더 작아진다는 특징이 있습니다.
3.평균 구하기
다음과 같이 A반 의 수학 과 과학 점수가 있다고 해봅시다.
| A반성적 | 수학 | 과학 |
| 김남주 | 100 | 95 |
| 박석희 | 54 | 60 |
| 이세성 | 74 | 82 |
| 한지혜 | 80 | 95 |
| 신보은 | 66 | 72 |
| 석호필 | 98 | 100 |
| 최아라 | 88 | 84 |
| 윤서향 | 74 | 95 |
| 임혁 | 98 | 100 |
A반은 수학과 과학 중에서 어떤 것을 더 잘한다고 할 수 있을까요?
이럴 때 사용하는 것이 평균 입니다.
평균을 구하기 위해서 위의 설명대로 모든 숫자들을 일일히 비교해볼 필요는 없습니다.
여러가지 숫자들의 평균을 편하게 구하기 위해선 이 공식을 사용하게됩니다.
▷공식이란 수학의 결과를 편하게 구하기 위해서 정리되어있는 계산순서를 의미합니다.

수학 점수를 예시로 들면 이렇게 됩니다.
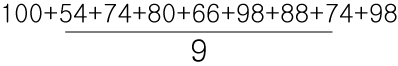
합한 '결과' 에서 갯수를 나누는 것 이기 때문에, 먼저 덧셈 결과를 구해줍시다.
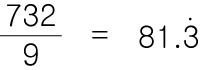
그리고 이것을 계산해본다면 결과로는 81.333 이라는 값이 나옵니다.
마찬가지로 과학도 평균을 구해본다면 87 이라는 값이 나옵니다.
즉, A 반은 과학을 수학보다 더 잘한다고 할 수 있습니다.
이때 평균은 높다 , 낮다 라는 말로 비교합니다.
이렇게 평균이란, 여러가지 데이터를 하나의 값으로 줄여서 표현하는 중요한 핵심인 것을 알 수 있습니다.
그리고 데이터를 하나로 줄였을 때에 쉽게 처리할 수 있는 여러 경우가 존재한다는 것도 알 수 있습니다.
평균은 데이터 압축의 핵심입니다. 반드시 숙지합시다.
4.중앙값의 개념
중앙값은 초5과정이 아니지만 꼭 평균과 같이 설명해야하는 특징이 있으므로 빠르게 알아봅시다.

3 과 26의 평균은 14.5 입니다.
그리고 지닌 숫자들 중에서 14.5에 가장 가까운 숫자는 15입니다.
이 숫자들 안에서 중앙에 위치한 값은 15 라고 할수 있습니다.

중앙 값은 2개이상 존재할 수도 있습니다. 보통은 둘중의 하나를 선택해서 사용합니다.
혹은 15 와 16의 평균인 15.5를 중앙값으로 쓸 수 있습니다.