[미분] 도함수의 활용과 정리
본 내용은 주로 접선과 그래프 성질을 다루고 있습니다.
접선의 방정식과 관련된 예제가 없습니다.
접선 과목의 특성상 주로 그래프와 도형 해석 능력을 중심으로 합니다.
문제들을 들고와서 닮음 , 기울기 곱이 -1, 축의방정식 등을 일일히 집는것이 범위를 초과하기도 하며,
스스로의 발견 능력이 중요하기 때문에 누군가가 알려준다면 근본적으로 해결이 안돼기 때문입니다.
1.개념
[접선]
1.접선의 방정식
미분계수가 하나의 점에 대한 순간 기울기라면
순간 기울기와 특정 좌표의 직선의 방정식을 통해서 접선의 방정식을 구할 수 있습니다.

x²-4x 위를 지나가는 점 (5,5) 에대한 접선의 방정식을 구한다면
도함수가 f'(x) = 2x-4 일때 f'(5)=6
그러므로 직선의 방정식의 기울기 a=6일때
접선의 방정식은 y=6(x-5)+5 가 됩니다.
2.접하는 두 함수식의 성질
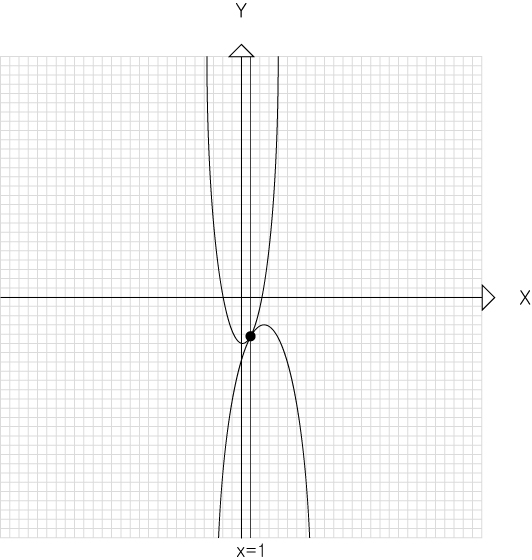
①두 함수가 x=1 에서 접할 경우
f(1)=g(1) , f'(1)=g'(1) 가 성립합니다.
역으로 f(1)=g(1) , f'(1)=g'(1) 일때 두 함수는 접합니다.
그러므로 접하는 두 함수에 대해선 등식이 성립하며,
이를 통해서 식에 존재하는 미지수 a를 f(1)=g(1) , f'(1)=g'(1) 의 연립방정식으로 알수 있습니다.
②두 함수가 접하지 않을 경우
서로 접하지 않지만 f'(a)=g'(b) 를 충족한다면
a~b의 유클리드 거리는 두 함수간의 최소 거리가 됩니다.
[정리]
1.롤의 정리

[a,b] 연속 , (a,b)미분 가능할 때, ƒ(a)=ƒ(b) 라면
ƒ'(c)=0 (기울기가 0, 수평) 인 구간이 (a,b)안에 반드시 존재합니다.
2.평균값 정리 (MVT)

[a,b] 연속 , (a,b)미분 가능할때
f'(c)=y(b-a)/x(b-a) 인 구간이 (a,b)안에 존재합니다.

쉽게 말해서 a,b의 두점사이의 기울기를 m 이라고 한다면
함수내에서 f'(c)=m 인 구간이 a,b의 범위안에 존재한다는 의미입니다.
3.기타 그래프 성질
① 모든 구간에서 f'(x)=0 일때 상수함수
② ƒ'(x)=g'(x) 일때 ƒ(x)=g(x)+C
4.나머지정리와 도함수의 구조
ƒ(x) ÷ (x-a)³ 에 대해서 몱Q(x), 나머지R(x), 나눈 값 (x-a)³ 로 f(x)를 표현한다면
ƒ(x)=(x-a)³Q(x)+R(x)
그렇다면 이에 대한 도함수 ƒ'(x)는
ƒ'(x)=3(x-a)²Q(x)(x-a)'+(x-a)³Q'(x)+R'(x) 로 정리됩니다.
이를 정리해서
ƒ'(x) = (x-a)²T(x)+R'(x) 라고 한다면, (T(x)는 정리된 인자들의 곱묶음)
ƒ'(a) = R'(a) 입니다.
ƒ(a)=R(a) 이므로 ƒ'(a)=R'(a) 로 이해하면 빠릅니다.
완전제곱식으로 나눈 값으로 표현한 ƒ(x) = (x-a)ⁿQ(x)의 도함수 ƒ'(x)는
(x-a)ⁿ⁻¹ 가 반드시 인수로 존재한다는 점을 기억해둡시다.
2.응용
[추가지식]
1.완전제곱식에의한 접선의 최고 기울기
ƒ'(x)를 완전 제곱식으로 표현해서
-3(x-3)²+15 일때 최고 기울기는 k=15 입니다.
2.두 함수 기울기가 서로 수직일때
ƒ'(x)g'(x)=-1
[기본]
1.롤의 정리 예제
ƒ(-1)=ƒ(3) 일때 롤의 정리에의해 ƒ(c)=0이 존재합니다.
ƒ'(x) 에 c를 대입해서
ƒ'(c)=3c²-2c-5=0 → (c+1)(3c-5)=0
이라고 할때, -1~3범위내에 존재하는 c=5/3 입니다.
2.평균값 정리 예제
ƒ(x)에 대해서 x=2 일때 y값은 f(2) , x=-3 일때 y값은 f(-3)
그러므로 이에 대한 기울기를 구하면 아래와 같습니다.

식을 정리한 뒤엔 필요하다면 인수분해를 한 뒤에 범위내의 c를 찾습니다.
[심화]
1.두함수의 접하는 근 {다소 이해력 필요}
근의 지점에서 접선의 방정식이 서로 같을때 등식에서 한쪽을 0으로 밀어서
ƒ'(a)-g'(a)=0이라고 한다면 ,
이때 ƒ'(x)-g'(x)=0 의 근, 즉 0으로 만드는 수는 x=a입니다.
두함수가 접할때 ƒ'(a)=g'(a) , ƒ(a)=g(a) 이므로
마찬가지로 ƒ(x)-g(x)=0 의 근은 x=a입니다.
그래서 만약 두함수 접하는게 확실하고 지점만을 모른다면
ƒ'(x)-g'(x)=0 과 ƒ(x)-g(x)=0 의 연립방정식으로 a를 구할 수 있습니다.